
分析 如图,过点E作FK∥x轴,BF⊥FK于F,DK⊥FK于K,AM⊥FK于M.首先求出点E坐标,推出AM=2,EM=$\frac{3}{2}$,由△AME≌△EKD≌△EFB,可得EK=EF=AM=2,DK=BF=EM=$\frac{3}{2}$,由此即可解决问题.
解答 解:如图,过点E作FK∥x轴,BF⊥FK于F,DK⊥FK于K,AM⊥FK于M.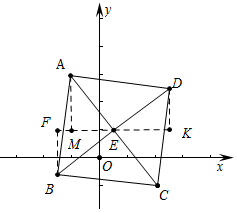
∵四边形ABCD是正方形,A(-1,3),C(2,-1),
∴EA=EC=EB=ED,E($\frac{1}{2}$,1),
∴AM=2,EM=$\frac{3}{2}$,
由△AME≌△EKD≌△EFB,可得EK=EF=AM=2,DK=BF=EM=$\frac{3}{2}$,
∴D($\frac{5}{2}$,$\frac{5}{2}$),B(-$\frac{3}{2}$,-$\frac{1}{2}$)或B($\frac{5}{2}$,$\frac{5}{2}$),D(-$\frac{3}{2}$,-$\frac{1}{2}$).
点评 本题考查正方形的性质、全等三角形的判定和性质、中点坐标公式等知识,解题的关键是学会添加常用辅助线构造全等三角形解决问题,属于中考常考题型.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:解答题
| 购票张数 | 1-50张 | 51~100张 | 100张以上 |
| 每张票价 | 13元 | 11元 | 9元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com