
【题目】已知抛物线![]() .
.
![]() 求该抛物线的对称轴和顶点P的坐标.
求该抛物线的对称轴和顶点P的坐标.
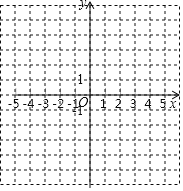
![]() 在图中的直角坐标系内用五点法画出该抛物线的图象.
在图中的直角坐标系内用五点法画出该抛物线的图象.
![]() 将该抛物线向下平移2个单位,向左平移3个单位得到抛物线
将该抛物线向下平移2个单位,向左平移3个单位得到抛物线![]() ,此时点P的对应点为
,此时点P的对应点为![]() ,试求直线
,试求直线![]() 与y轴的交点坐标.
与y轴的交点坐标.
 每课必练系列答案
每课必练系列答案科目:初中数学 来源: 题型:
【题目】如图1,定义:在直角三角形ABC中,锐角α的邻边与对边的比叫做角α的余切,记作ctanα,即ctanα=![]() =
=![]() ,根据上述角的余切定义,解下列问题:
,根据上述角的余切定义,解下列问题:
(1)如图1,若BC=3,AB=5,则ctanB= ;
(2)ctan60°= ;
(3)如图2,已知:△ABC中,∠B是锐角,ctan C=2,AB=10,BC=20,试求∠B的余弦cosB的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我省松原地震后,某校开展了“我为灾区献爱心”捐款活动,八年级一班的团支部对全班50人捐款数额进行了统计,绘制出如下的统计图.
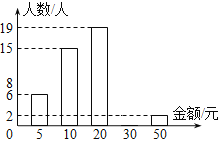
(1)把统计图补充完整;
(2)直接写出这组数据的众数和中位数;
(3)若该校共有学生1600人,请根据该班的捐款情况估计该校捐款金额为20元的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
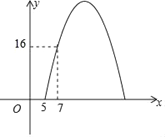
【题目】某商场经调研得出某种商品每天的利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx﹣75,其图象如图所示.
(1)求a与b的值;
(2)销售单价为多少元时,该种商品每天的销售利润最大?最大利润是多少元?(参考公式:当x=![]() 时,二次函数y=ax2+bx+c(a≠0)有最小(大)值)
时,二次函数y=ax2+bx+c(a≠0)有最小(大)值)
(3)销售单价定在多少时,该种商品每天的销售利润为21元?结合图象,直接写出销售单价定在什么范围时,该种商品每天的销售利润不低于21元?
查看答案和解析>>
科目:初中数学 来源: 题型:
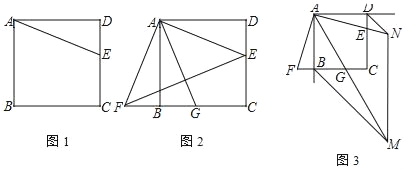
【题目】如图,点E是正方形ABCD中CD边上任意一点,AB=4,以点A为中心,把△ADE顺时针旋转90°得到△AD′F
(1)画出旋转后的图形,求证:点C、B、F三点共线;
(2)AG平分∠EAF交BC于点G.
①如图2,连接EF.若BG:CE=5:6,求△AEF的面积;
②如图3,若BM、DN分别为正方形的两个外角角平分线,交AG、AE的延长线于点M、N.当MM∥DC时,直接写出DN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=14.5米,NF=0.2米.设太阳光线与水平地面的夹角为α,当α=56.3°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的NF这层上晒太阳.

(1)求楼房的高度约为多少米?
(2)过了一会儿,当α=45°时,问小猫能否还晒到太阳?请说明理由.(参考数据:sin56.3°≈0.83,cos56.3°≈0.55,tan56.3°≈1.5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+ax+b=0(b≠0)与x2+cx+d=0都有实数根,若这两个方程有且只有一个公共根,且ab=cd,则称它们互为“同根轮换方程”.如x2-x-6=0与x2-2x-3=0互为“同根轮换方程”.
(1)若关于x的方程x2+4x+m=0与x2-6x+n=0互为“同根轮换方程”,求m的值;
(2)已知方程①:x2+ax+b=0和方程②:x2+2ax+![]() b=0,p、q分别是方程①和方程②的实数根,且p≠q,b≠0.试问方程①和方程②是否能互为“同根轮换方程”?如果能,用含a的代数式分别表示p和q;如果不能,请说明理由.
b=0,p、q分别是方程①和方程②的实数根,且p≠q,b≠0.试问方程①和方程②是否能互为“同根轮换方程”?如果能,用含a的代数式分别表示p和q;如果不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com