
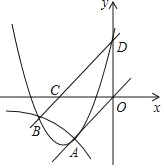
【题目】如图,已知正比例函数和反比例函数的图象都经过点A(﹣3,﹣3).
(1)求正比例函数和反比例函数的表达式;
(2)把直线OA向上平移后与反比例函数的图象交于点B(﹣6,m),与x轴交于点C,求m的值和直线BC的表达式;
(3)在(2)的条件下,直线BC与y轴交于点D,求以点A,B,D为顶点的三角形的面积;
(4)在(3)的条件下,点A,B,D在二次函数的图象上,试判断该二次函数在第三象限内的图象上是否存在一点E,使四边形OECD的面积S1与四边形OABD的面积S满足:S1=![]() S?若存在,求点E的坐标;若不存在,请说明理由.
S?若存在,求点E的坐标;若不存在,请说明理由.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]() ;(4)E的坐标是(﹣2,﹣
;(4)E的坐标是(﹣2,﹣![]() ).
).
【解析】
(1)利用待定系数法即可求得函数的解析式;
(2)把B(﹣6,m)代入反比例函数解析式即可求出m的值,再根据直线平移的性质即可求直线BC的表达式;
(3)作AM⊥y轴于点M,作BN⊥y轴于点N,根据S四边形ABDM=S梯形ABNM+S△BDN,S△ABD=S四边形ABDM﹣S△ADM即可求解;
(4)设二次函数的解析式是y=ax2+bx+![]() ,然后利用待定系数法求得二次函数的解析式,根据S1=
,然后利用待定系数法求得二次函数的解析式,根据S1=![]() S即可求得S1的值,根据S1=S△OCD+S△OCE列方程求出y0的值,再由E(x0,y0)在二次函数的图象上,即可求得x0的值,进而求得E的坐标.
S即可求得S1的值,根据S1=S△OCD+S△OCE列方程求出y0的值,再由E(x0,y0)在二次函数的图象上,即可求得x0的值,进而求得E的坐标.
解:(1)设正比例函数的解析式是y=kx,代入(﹣3,﹣3),得:﹣3k=﹣3,解得:k=1,
则正比例函数的解析式是:y=x;
设反比例函数的解析式是y=![]() ,把(﹣3,﹣3)代入解析式得:k1=9,
,把(﹣3,﹣3)代入解析式得:k1=9,
则反比例函数的解析式是:y=![]() ;
;
(2)m=![]() =﹣
=﹣![]() ,则点B的坐标是(﹣6,﹣
,则点B的坐标是(﹣6,﹣![]() ),
),
∵y=k3x+b的图象是由y=x平移得到,
∴k3=1,即y=x+b,
故一次函数的解析式是:y=x+![]() ;
;
(3)∵y=x+![]() 的图象交y轴于点D,
的图象交y轴于点D,
∴D的坐标是(0,![]() ),
),
作AM⊥y轴于点M,作BN⊥y轴于点N.
∵A的坐标是(﹣3,﹣3),B的坐标是(6,﹣![]() ),
),
∴M的坐标是(0,﹣3),N的坐标是(0,﹣![]() ).
).
∴OM=3,ON=![]() .
.
则MD=3+![]() =
=![]() ,DN=
,DN=![]() +
+![]() =6,MN=3﹣
=6,MN=3﹣![]() =
=![]() .
.
则S△ADM=![]() ×3×
×3×![]() =
=![]() ,S△BDN=
,S△BDN=![]() ×6×6=18,S梯形ABNM=
×6×6=18,S梯形ABNM=![]() ×(3+6)×
×(3+6)×![]() =
=![]() .
.
则S四边形ABDM=S梯形ABNM+S△BDN=![]() +18=
+18=![]() ,
,
S△ABD=S四边形ABDM﹣S△ADM=![]() ﹣
﹣![]() =
=![]() ;
;
(4)设二次函数的解析式是y=ax2+bx+![]() ,
,
则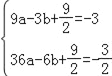 ,
,
解得:![]() ,
,
则这个二次函数的解析式是:y=![]() x2+4x+
x2+4x+![]() ;
;
点C的坐标是(﹣![]() ,0).
,0).
则S=![]() ×6﹣
×6﹣![]() ×6×6﹣
×6×6﹣![]() ×3×
×3×![]() ﹣
﹣![]() ×3×
×3×![]() =45﹣18﹣
=45﹣18﹣![]() ﹣
﹣![]() =
=![]() .
.
假设存在点E(x0,y0),使S1=![]() S=
S=![]() ×
×![]() =
=![]() .
.
∵四边形CDOE的顶点E只能在x轴的下方,
∴y0<0,
∴S1=S△OCD+S△OCE=![]() ×
×![]() ×
×![]() ﹣
﹣![]() ×
×![]() y0=
y0=![]() ﹣
﹣![]() y0,
y0,
∴![]() ﹣
﹣![]() y0=
y0=![]() ,
,
∴y0=﹣![]() ,
,
∵E(x0,y0)在二次函数的图象上,
∴![]() x02+4x0+
x02+4x0+![]() =﹣
=﹣![]() ,
,
解得:x0=﹣2或﹣6.
当x0=﹣6时,点E(﹣6,﹣![]() )与点B重合,这时CDOE不是四边形,故x0=﹣6(舍去).
)与点B重合,这时CDOE不是四边形,故x0=﹣6(舍去).
∴E的坐标是(﹣2,﹣![]() ).
).


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形(各边相等,各内角为直角),E是BC边上一点,F是CD上的一点.
(1)若△CFE的周长等于正方形ABCD的周长的一半,求证:∠EAF=45°;
(2)在(1)的条件下,若DF=2,CF=4,CE=3,求△AEF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线交于点O,点E、F分别在AB、BC上(AE<BE),且∠EOF=90°,OE、DA的延长线交于点M,OF、AB的延长线交于点N,连接MN.
(1)求证:OM=ON.
(2)若正方形ABCD的边长为4,E为OM的中点,求MN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条街AB上,甲由A向B步行,乙骑车由B向A行驶,乙的速度是甲的速度的3倍,此时公共汽车由始发站A开出向B行进,且每隔x分发一辆车,过了一段时间,甲发现每隔10分有一辆公共汽车追上他,而乙感到每隔5分就碰到一辆公共汽车,那么在始发站公共汽车发车的间隔时间x=_____分钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
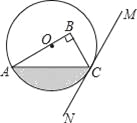
【题目】如图,在Rt△ABC中,∠B=90°,点O在边AB上,以点O为圆心,OA为半径的圆经过点C,过点C作直线MN,使∠BCM=2∠A.
(1)判断直线MN与⊙O的位置关系,并说明理由;
(2)若OA=4,∠BCM=60°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D为BC的中点,DE⊥BC交∠BAC的平分线AE于E,EF⊥AB于F,EG⊥AC交AC的延长线于G,AB=5,AC=3.求CG.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF.
(1)求△ABE的面积.
(2)求折痕EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,共享单车服务的推出(如图1),极大的方便了城市公民绿色出行,图2是某品牌某型号单车的车架新投放时的示意图(车轮半径约为30cm),其中BC∥直线l,∠BCE=71°,CE=54cm.
(1)求单车车座E到地面的高度;(结果精确到1cm)
(2)根据经验,当车座E到CB的距离调整至等于人体胯高(腿长)的0.85时,坐骑比较舒适.小明的胯高为70cm,现将车座E调整至座椅舒适高度位置E′,求EE′的长.(结果精确到0.1cm)
(参考数据:sin71°≈0.95,cos71°≈0.33,tan71°≈2.90)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com