
科目:初中数学 来源: 题型:解答题
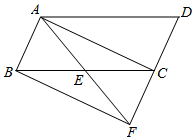 如图,已知平行四边形ABCD中,E是BC的中点,连接AE并延长,交DC的延长线于点F,且AF=AD,连接BF,求证:四边形ABFC是矩形.
如图,已知平行四边形ABCD中,E是BC的中点,连接AE并延长,交DC的延长线于点F,且AF=AD,连接BF,求证:四边形ABFC是矩形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
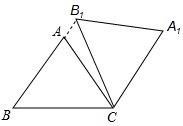 在△ABC中,AB=AC=5,cos∠ABC=$\frac{3}{5}$,将△ABC绕点C顺时针旋转,得到△A1B1C,且点B1在线段BA延长线上(如图).
在△ABC中,AB=AC=5,cos∠ABC=$\frac{3}{5}$,将△ABC绕点C顺时针旋转,得到△A1B1C,且点B1在线段BA延长线上(如图).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
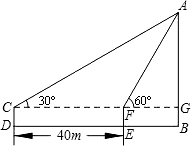 上完《解直角三角形》这章后,一次数学课外活动时,数学兴趣小组的张进、阿芬和晓晨等人在校园里测量如图所示的教学楼的高度AB.
上完《解直角三角形》这章后,一次数学课外活动时,数学兴趣小组的张进、阿芬和晓晨等人在校园里测量如图所示的教学楼的高度AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
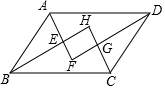 如图,在?ABCD中,AF、BH、CH、DF分别是∠DAB、∠ABC、∠BCD、∠CDA的平分线,AF与BH交于点E,CH与DF交于点G.在不添加其他条件的情况下,试写出上述条件推出的结论,并选择你喜欢的一个结论说明成立的理由.(要求推理过程中用到″平行四边形″和″角平分线″这两个条件).
如图,在?ABCD中,AF、BH、CH、DF分别是∠DAB、∠ABC、∠BCD、∠CDA的平分线,AF与BH交于点E,CH与DF交于点G.在不添加其他条件的情况下,试写出上述条件推出的结论,并选择你喜欢的一个结论说明成立的理由.(要求推理过程中用到″平行四边形″和″角平分线″这两个条件).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
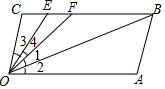 如图所示,已知射线CB∥OA,∠C=∠OAB=120°,E、F在CB上,且∠1=∠2,∠3=∠4.
如图所示,已知射线CB∥OA,∠C=∠OAB=120°,E、F在CB上,且∠1=∠2,∠3=∠4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ③ | D. | ①③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com