
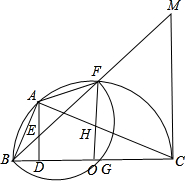
 如图所示,已知BC是半圆O的直径,△ABC内接于⊙O,以A为圆心,AB为半径作弧交⊙O于F,交BC于G,交OF于H,AD⊥BC于D,AD、BF交于E,CM切⊙O于C,交BF的延长线于M,若FH=6,AE=
如图所示,已知BC是半圆O的直径,△ABC内接于⊙O,以A为圆心,AB为半径作弧交⊙O于F,交BC于G,交OF于H,AD⊥BC于D,AD、BF交于E,CM切⊙O于C,交BF的延长线于M,若FH=6,AE=| 5 | 3 |
 |
| AB |
 |
| AF |
 |
| AF |
 |
| BN |
| 3 |
| 4 |
| ED |
| BD |
| MC |
| BC |
| 3k |
| 4k |
| MC |
| 20k |
| 3 |
| 4 |
| 27 |
| 4 |


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:
 (2013•成都一模)如图所示,已知BC是⊙O的直径,A、D是⊙O上的两点.
(2013•成都一模)如图所示,已知BC是⊙O的直径,A、D是⊙O上的两点. |
| CD |
| 1 |
| 2 |
 |
| AC |
| 2 |
| BC•CE |
| AB |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,已知BC是半圆O的直径,△ABC内接于⊙O,以A为圆心,AB为半径作弧交⊙O于F,交BC于G,交OF于H,AD⊥BC于D,AD、BF交于E,CM切⊙O于C,交BF的延长线于M,若FH=6,
如图所示,已知BC是半圆O的直径,△ABC内接于⊙O,以A为圆心,AB为半径作弧交⊙O于F,交BC于G,交OF于H,AD⊥BC于D,AD、BF交于E,CM切⊙O于C,交BF的延长线于M,若FH=6,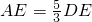 ,求FM的长.
,求FM的长.查看答案和解析>>
科目:初中数学 来源:2013年四川省成都市高新区中考数学一模试卷(解析版) 题型:解答题
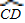 =
= 时,连接CD、AD,其中AD与直径BC相交于点E,求证:2CD2=CE•BC;
时,连接CD、AD,其中AD与直径BC相交于点E,求证:2CD2=CE•BC; ,求
,求 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2011年中考数学总复习专题:转化思想在代数中的应用2(解析版) 题型:解答题
 ,求FM的长.
,求FM的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com