
| 11 |
| 2 |
| 11 |
| 2 |
| 11 |
| 2 |
| 11 |
| 2 |
| 11 |
| 2 |
| 25 |
| 4 |
| 11 |
| 2 |
| 5 |
| 2 |
| 11 |
| 2 |
| 5 |
| 2 |
| 11 |
| 2 |
| 5 |
| 2 |
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:数学教研室 题型:044
通过本节课的学习,我们已经会对某些形如x2+px+q型二次三项式进行因式分解,此类多项式的特点是二次项的系数为1,如二次项的系数不为1,比如多项式3x2+11x+10又如何分解呢?
我们知道(x+2)(3x+5)=3x2+11x+10.反过来,就得到3x2+11x+10的因式分解的形式,即3x2+11x+10=(x+2)(3x+5).
我们发现,二次项的系数3分解成1、3两个因数的积;常数项10分解成2、5两个因数的积;当我们把1、3、2、5写成
1
![]()
![]() 2
2
3 5
后发现1×5+2×3恰好等于一次项的系数11.
像这种借助画十字交叉线分解系数,从而帮助我们把二次三项式分解因式的方法,通常叫做十字相乘法.
请用十字相乘法将下列各式分解因式:
(1)2x2-7x+3; (2)3a2-8a+4;
(3)6y2-11y-10; (4)5a2b2+23ab-10.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
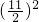 ,再减去这个数
,再减去这个数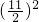 ,则:
,则: =
=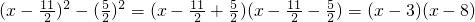 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com