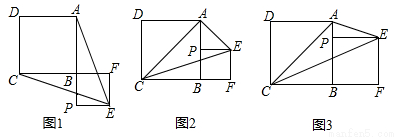
已知正方形ABCD，P为射线AB上的一点，以BP为边作正方形BPEF，使点F在线段CB的延长线上，连接EA、EC．
(1)如图1，若点P在线段AB的延长线上，求证：EA=EC；
(2)若点P在线段AB上．
①如图2，连接AC，当P为AB的中点时，判断△ACE的形状，并说明理由；
②如图3，设AB=a，BP=b，当EP平分∠AEC时，求a：b及∠AEC的度数．
科目：初中数学 来源：2016年初中毕业升学考试（山东烟台卷）数学（解析版） 题型：解答题
【探究证明】
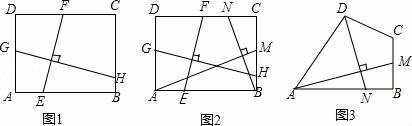
（1）某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究，提出下列问题，请你给出证明．
如图1，矩形ABCD中，EF⊥GH，EF分别交AB，CD于点E，F，GH分别交AD，BC于点G，H．求证：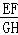
=
；
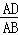【结论应用】
（2）如图2，在满足（1）的条件下，又AM⊥BN，点M，N分别在边BC，CD上，若=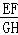
，则
的值为 ；
【联系拓展】
（3）如图3，四边形ABCD中，∠ABC=90°，AB=AD=10，BC=CD=5，AM⊥DN，点M，N分别在边BC，AB上，求
的值．
查看答案和解析>>
科目：初中数学 来源：2016年初中毕业升学考试（山东济宁卷）数学（解析版） 题型：选择题
如图，在⊙O中，
=
，∠AOB=40°，则∠ADC的度数是（ ）
A．40° B．30° C．20° D．15°
查看答案和解析>>
科目：初中数学 来源：2016年初中毕业升学考试（山东滨州卷）数学（解析版） 题型：选择题
如图，AB是⊙O的直径，C，D是⊙O上的点，且OC∥BD，AD分别与BC，OC相交于点E，F，则下列结论：
①AD⊥BD；②∠AOC=∠AEC；③CB平分∠ABD；④AF=DF；⑤BD=2OF；⑥△CEF≌△BED，其中一定成立的是（ ）
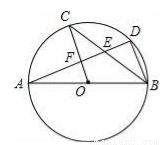
A．②④⑤⑥ B．①③⑤⑥ C．②③④⑥ D．①③④⑤
查看答案和解析>>
科目：初中数学 来源：2016年初中毕业升学考试（山东滨州卷）数学（解析版） 题型：选择题
某校男子足球队的年龄分布如图所示，则根据图中信息可知这些队员年龄的平均数，中位数分别是（ ）
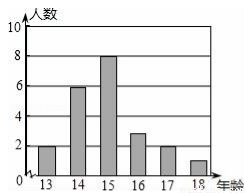
A．15.5，15.5 B．15.5，15 C．15，15.5 D．15，15
查看答案和解析>>
科目：初中数学 来源：2016年初中毕业升学考试（江苏泰州卷）数学（解析版） 题型：解答题
随着互联网的迅速发展，某购物网站的年销售额从2013年的200万元增加到2015年的392万元.求该购物网站平均每年销售额增长的百分率.
查看答案和解析>>
科目：初中数学 来源：2016年初中毕业升学考试（江苏泰州卷）数学（解析版） 题型：填空题
如图，△ABC中，BC=5cm，将△ABC沿BC方向平移至△A’B’C’的位置时，A’B’恰好经过AC的中点O，则△ABC平移的距离为 cm.
查看答案和解析>>
科目：初中数学 来源：2015-2016学年江苏省江阴市七年级下第一次月考数学试卷（解析版） 题型：解答题
课本拓展
旧知新意：
我们容易证明，三角形的一个外角等于与它不相邻的两个内角的和．那么，三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢？
1．尝试探究：
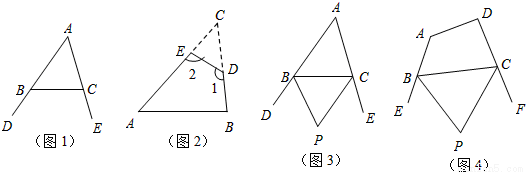
（1）如图1，∠DBC与∠ECB分别为△ABC的两个外角，试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系？为什么？
2．初步应用：
（2）如图2，在△ABC纸片中剪去△CED，得到四边形ABDE，∠1=130°，则∠2-∠C= ；
（3）小明联想到了曾经解决的一个问题：如图3，在△ABC中，BP、CP分别平分外角∠DBC、∠ECB，∠P与∠A有何数量关系？请利用上面的结论直接写出答案 ．
3拓展提升：
（4）如图4，在四边形ABCD中，BP、CP分别平分外角∠EBC、∠FCB，∠P与∠A、∠D有何数量关系？为什么？（若需要利用上面的结论说明，可直接使用，不需说明理由）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
