
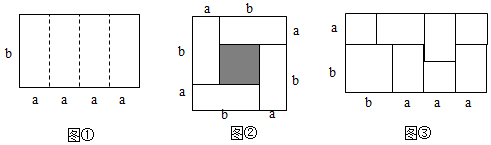
���� ��1����Ӱ����Ϊ�߳�Ϊ��b-a���������Σ�Ȼ����������ε������ʽ��⣻
��2����ͼ2�У�����������С�����κ�4��������ɣ���a+b��2-��a-b��2=4ab��
��3���ɣ�2���Ľ��۵õ���x+y��2-��x-y��2=4xy���ٰ�x+y=4��x•y=$\frac{9}{4}$�õ���x-y��2=7��
��4���۲�ͼ�εõ��߳�Ϊ��a+b���루3a+b���ľ�����3���߳�Ϊa�������Ρ�4���߳�Ϊa��b�ľ��κ�һ���߳�Ϊb����������ɣ����У�a+b��•��3a+b��=3a2+4ab+b2��
��� �⣺��1����Ӱ����Ϊ�߳�Ϊ��b-a���������Σ�������Ӱ���ֵ������b-a��2��
�ʴ�Ϊ����b-a��2��
��2��ͼ2�У��ñ߳�Ϊa+b�������ε������ȥ�߳�Ϊb-a�������ε���4�������ֱ�a��b�ľ��������
���ԣ�a+b��2-��a-b��2=4ab��
�ʴ�Ϊ����a+b��2-��a-b��2=4ab��
��3���ߣ�x+y��2-��x-y��2=4xy��
��x+y=4��x•y=$\frac{9}{4}$��
��42-��x-y��2=4��$\frac{9}{4}$��
�ࣨx-y��2=7��
�ʴ�Ϊ��7��
��4���߳�Ϊ��a+b���루3a+b���ľ������Ϊ��a+b����3a+b��������3���߳�Ϊa�������Ρ�4���߳�Ϊa��b�ľ��κ�һ���߳�Ϊb����������ɣ�
�ࣨa+b��•��3a+b��=3a2+4ab+b2��
�ʴ�Ϊ����a+b��•��3a+b��=3a2+4ab+b2��
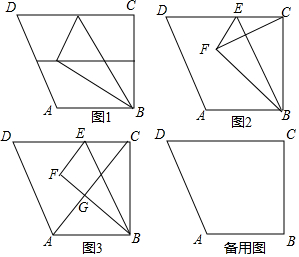
���� ���⿼������ȫƽ����ʽ�ļ��α��������������֤����ȫƽ����ʽ��a-b��2=a2-2ab+b2��


 ��ʦָ����ĩ��̾�ϵ�д�
��ʦָ����ĩ��̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
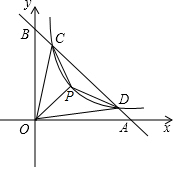 ��ͼ����֪C��D�Ƿ���������y=$\frac{m}{x}$ͼ���ڵ�һ�����ڵķ�֧�ϵ����㣬ֱ��CD�ֱ�x�ᣬy����A��B���㣬��C��D������ֱ��ǣ�x1��y1������x2��y2��������OC��OD��
��ͼ����֪C��D�Ƿ���������y=$\frac{m}{x}$ͼ���ڵ�һ�����ڵķ�֧�ϵ����㣬ֱ��CD�ֱ�x�ᣬy����A��B���㣬��C��D������ֱ��ǣ�x1��y1������x2��y2��������OC��OD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ABΪ��O��ֱ����ACΪ�ң�OD��BC��AC�ڵ�D����BC=20cm����OD=10cm��
��ͼ��ABΪ��O��ֱ����ACΪ�ң�OD��BC��AC�ڵ�D����BC=20cm����OD=10cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 С����С����С�ա�Сӱһ���о�һ����ѧ�⣬��ͼ����֪EF��AB��CD��AB��
С����С����С�ա�Сӱһ���о�һ����ѧ�⣬��ͼ����֪EF��AB��CD��AB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com