
分析 (1)根据二次根式的乘除法进行计算即可;
(2)先对原式化简,再合并同类项即可解答本题;
(3)根据多项式乘以多项式的方法进行计算即可解答本题;
(4)根据完全平方公式即可解答本题.
解答 解:(1)2$\sqrt{12}×\frac{\sqrt{3}}{4}÷\sqrt{2}$
=$4\sqrt{3}×\frac{\sqrt{3}}{4}×\frac{1}{\sqrt{2}}$
=$\frac{3}{\sqrt{2}}$
=$\frac{3\sqrt{2}}{2}$;
(2)$\sqrt{12}-\sqrt{18}-\sqrt{32}+\sqrt{48}$
=$2\sqrt{3}-3\sqrt{2}-4\sqrt{2}+4\sqrt{3}$
=$6\sqrt{3}-7\sqrt{2}$;
(3)(3$\sqrt{3}$+2$\sqrt{2}$)(2$\sqrt{3}-3\sqrt{2}$)
=$18-9\sqrt{6}+4\sqrt{6}-12$
=$6-5\sqrt{6}$;
(4)(3$\sqrt{6}$-$\sqrt{15}$)2
=$(3\sqrt{6})^{2}-6\sqrt{90}+(\sqrt{15})^{2}$
=54-$18\sqrt{10}$+15
=$69-18\sqrt{10}$.
点评 本题考查二次根式的混合运算,解题的关键是明确二次根式的混合运算的计算方法.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:解答题
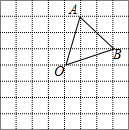 如图,在边长为1的小正方形组成的网格中,△AOB的三个顶点均在格点上,点A、B的坐标分别是A(1,3),B(3,1).
如图,在边长为1的小正方形组成的网格中,△AOB的三个顶点均在格点上,点A、B的坐标分别是A(1,3),B(3,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.037×1010元 | B. | 2.037×1011元 | C. | 2.037×1012元 | D. | 20.37×1010元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k<0 | B. | k<-1 | C. | k<-2 | D. | k<-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
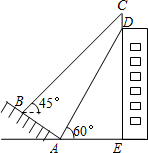 如图,百货大楼的顶部竖有一根“避雷针”CD,甲同学在距离大楼墙根E处30米的山坡的坡脚A处测得“避雷针”底部的D的仰角为60°,沿山坡向上走到B处测得“避雷针”顶部C的仰角为45°.已知山坡AB的坡度i=1:$\sqrt{3}$,AB=20米,求“避雷针”CD的高度.(测角器的高度忽略不计,结果精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,百货大楼的顶部竖有一根“避雷针”CD,甲同学在距离大楼墙根E处30米的山坡的坡脚A处测得“避雷针”底部的D的仰角为60°,沿山坡向上走到B处测得“避雷针”顶部C的仰角为45°.已知山坡AB的坡度i=1:$\sqrt{3}$,AB=20米,求“避雷针”CD的高度.(测角器的高度忽略不计,结果精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com