解:(1)由题意知:抛物线的对称轴为:x=1,则B(3,0);
已知OB=OC=3,则C(0,-3);
设抛物线的解析式为:y=a(x-1)(x-3),依题意有:
a(0-1)(0-3)=-3,a=-1;
故抛物线的解析式为:y=-x
2+4x-3.
(2)设AE交y轴于点F;
易证得△FOA∽△FEC,有
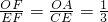
,

设OF=x,则EF=3x,
所以FA=3x-1;
在Rt△FOA中,由勾股定理得:
(3x-1)
2=x
2+1,
解得x=

;
即OF=

,F(0,

);
求得直线AE为y=-

x+

,联立抛物线的解析式得:
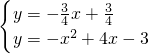
,
解得
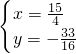
,
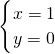
;
故点P(
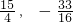
).
(3)∵B(3,0),C(0,-3),
∴直线BC:y=x-3;
设点M(a,a-3),则:
①当点M在第一象限时,OG=a,MG=a-3;

过M作MG⊥x轴于G,过N作NH⊥x轴于H;
根据旋转的性质知:∠MON=90°,OM=ON,
则可证得△MOG≌△NOH,得:
OG=NH=a,OH=MG=a-3,
故N(a-3,-a),
将其代入抛物线的解析式中,得:
-(a-3)
2+4(a-3)-3=-a,
整理得:a
2-11a+24=0,
a=3(舍去),a=8;
故M(8,5),N(5,-8).
②当点M在第三象限时,OG=-a,MG=3-a;
同①可得:MG=OH=3-a,OG=NH=-a,则N(3-a,a),代入抛物线的解析式可得:
-(3-a)
2+4(3-a)-3=a,
整理得:a
2-a=0,故a=0,a=1;
由于点M在第三象限,
所以a<0,
故a=0、a=1均不合题意,此种情况不成立;
③当点M在第四象限时,OG=a,MG=3-a;
同①得:N(3-a,a),在②中已经求得此时a=0(舍去),a=1;
故M(1,-2),N(2,1);
综上可知:存在符合条件的N点,且坐标为N(2,1)或(5,-8).
分析:(1)根据抛物线的解析式,可得抛物线的对称轴方程,进而可根据点A的坐标表示出点B的坐标,已知OB=OC,即可得到点C的坐标,从而利用待定系数法求得抛物线的解析式.
(2)点P为直线AE和抛物线的交点,欲求点P,必须先求出直线AE的解析式;设直线AE与y轴的交点为F,易得△FOA∽△FEC,由于OA=1,EC=3,根据相似三角形的对应边成比例即可得到FE=3OF,设OF=x,则EF=3x,AF=3x-1,进而可在Rt△FOA中求出x的值,也就能求出F点的坐标,然后利用待定系数法求出直线AE的解析式,联立抛物线的解析式即可得到点P的坐标.
(3)此题应分三种情况讨论:
①当点M在第一象限时,可设M(a,a-3),由于ON是由OM旋转90°而得,因此△OMN是等腰直角三角形,分别过M、N作MG、NH垂直于x轴,即可证得△OMG≌△NOH,得MG=OH,NH=OG,由此可表示出N点的坐标,然后将其代入抛物线的解析式中,即可求得点M、N的坐标;
②当点M在第三象限,④点M在第四象限时,解法同①.
点评:此题考查了二次函数解析式的确定、函数图象交点坐标的求法、图形的旋转变化、全等三角形的判定和性质以及函数图象上点的坐标意义等知识.需要注意的是(3)题中,由于点M的位置不确定,一定要根据点M所处的不同象限分类讨论,以免漏解.

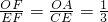 ,
,
 ;
; ,F(0,
,F(0, );
); x+
x+ ,联立抛物线的解析式得:
,联立抛物线的解析式得: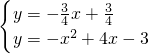 ,
,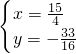 ,
,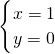 ;
;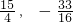 ).
).


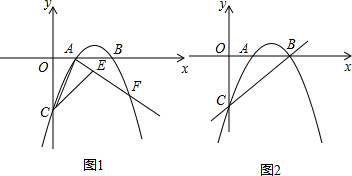
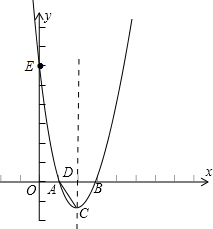 已知二次函数的图象是经过点A(1,0),B(3,0),E(0,6)三点的一条抛物线.
已知二次函数的图象是经过点A(1,0),B(3,0),E(0,6)三点的一条抛物线. 阅读材料:如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=
阅读材料:如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=
 如图,将抛物线y=-
如图,将抛物线y=-