
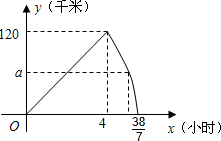
 甲、乙两车同时从A地出发,以各自的速度向B地行驶,甲车先到达B地,停留1小时后按原路以另一速度匀速返回,直到两车相遇.乙车的速度为每小时60千米.两车之间的距离y(千米)与乙车行驶时间x(小时)之间的函数图象如图所示.
甲、乙两车同时从A地出发,以各自的速度向B地行驶,甲车先到达B地,停留1小时后按原路以另一速度匀速返回,直到两车相遇.乙车的速度为每小时60千米.两车之间的距离y(千米)与乙车行驶时间x(小时)之间的函数图象如图所示.分析 (1)根据乙车的速度为每小时60千米乘以时间等于路程即可得到结论;
(2)根据乙车4小时行驶的路程加上甲乙两车4小时相距的距离等于A、B两地之间的距离是360km,根据距离除以时间等于速度即可得到距离;
(3)设从甲车返回到与乙车相遇过程中,y与x之间的函数关系式为y=kx+b.把(5,60),($\frac{38}{7}$,0)代入,即可得到结论;
(4)设甲车返回时的行驶速度为x千米/时.根据题意得到方程即可得到结果.
解答 解:(1)a=60×1=60,
故答案为:60;
(2)4×60+120=360(千米),360÷4=90(千米/时)
答:A、B两地之间的距离是360km,甲车从A到B的行驶速度是 90千米/时;
(3)设从甲车返回到与乙车相遇过程中,y与x之间的函数关系式为y=kx+b.
把(5,60),($\frac{38}{7}$,0)代入,得$\left\{\begin{array}{l}5k+b=60\\ \frac{38}{7}k+b=0.\end{array}\right.$,
解得 $\left\{\begin{array}{l}k=-140\\ b=760.\end{array}\right.$,
即从甲车返回到与乙车相遇过程中,y与x之间的函数关系式为y=-140x+760;
(4)设甲车返回时的行驶速度为x千米/时.
根据题意得;($\frac{38}{7}$-5)(x+60)=60,
解得 x=80,
即甲车返回时的行驶速度是80千米/时.
点评 本题主要考查了一次函数的应用,待定系数法求函数的解析式,一元一次方程的解法,解答时要注意数形结合思想的运用.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:解答题
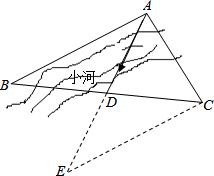 如图,在河的北岸种植一排小树AB,点C在河的南岸,已知在△ABC中,D是BC边的中点,AD的长度和方向都已确定,现在想要过点C也种植一排与AB平行的小树,小明使用了如下方法:延长AD到E,使DE=DA,连接 EC,那么就能得知AB∥EC,请你说明这样做的理由.
如图,在河的北岸种植一排小树AB,点C在河的南岸,已知在△ABC中,D是BC边的中点,AD的长度和方向都已确定,现在想要过点C也种植一排与AB平行的小树,小明使用了如下方法:延长AD到E,使DE=DA,连接 EC,那么就能得知AB∥EC,请你说明这样做的理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
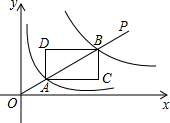 如图,在平面直角坐标系中,在第一象限过原点作射线OP,分别与函数y=$\frac{1}{x}$(x>0)和y=$\frac{9}{x}$(x>0)的图象交于点A、B点,以AB为对角线作矩形ACBD,且AC∥x轴,则矩形ACBD的面积为4.
如图,在平面直角坐标系中,在第一象限过原点作射线OP,分别与函数y=$\frac{1}{x}$(x>0)和y=$\frac{9}{x}$(x>0)的图象交于点A、B点,以AB为对角线作矩形ACBD,且AC∥x轴,则矩形ACBD的面积为4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
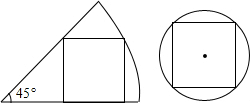 把一张圆形纸片和一张含45°角的扇形纸片如图所示的方式分别剪得一个正方形,如果所剪得的两个正方形边长都是1,那么圆形纸片和扇形纸片的面积比是( )
把一张圆形纸片和一张含45°角的扇形纸片如图所示的方式分别剪得一个正方形,如果所剪得的两个正方形边长都是1,那么圆形纸片和扇形纸片的面积比是( )| A. | 4:5 | B. | 2:5 | C. | $\sqrt{5}$:2 | D. | $\sqrt{5}$:$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 在装满红球的箱子里摸出一个白球是不确定事件 | |
| B. | 想了解重庆市民的幸福指数,宜采取抽样调查 | |
| C. | 某种福利彩票的中奖概率为$\frac{1}{10000}$,说明每买10000张彩票,一定有一张中奖 | |
| D. | 抛掷一枚图钉,钉尖朝上的概率是$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com