
 =PE·PO .
=PE·PO .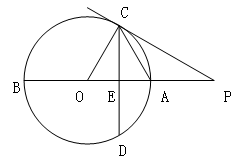
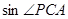 的值。
的值。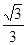
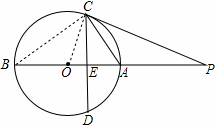
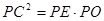 和∠P=∠P,可证得△PCO∽△PEC,即可证得∠PCO=∠PEC,再结合已知条件即可得出PC⊥OC,从而证得结论;
和∠P=∠P,可证得△PCO∽△PEC,即可证得∠PCO=∠PEC,再结合已知条件即可得出PC⊥OC,从而证得结论;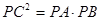 ,则
,则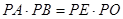 ,解一元二次方程即可求出x,从而得出⊙O的半径;
,解一元二次方程即可求出x,从而得出⊙O的半径;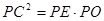
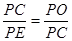
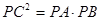
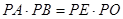
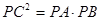
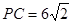
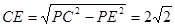
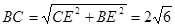
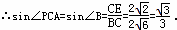


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:初中数学 来源:不详 题型:解答题
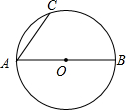
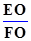 的值.
的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com