练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    平行四边形
    平行四边形
    、
    矩形
    矩形
    、
    正方形
    正方形
    都是中心对称图形．
    分析：根据中心对称图形的定义，从熟悉的图形中寻找．
    解答：解：平行四边形，矩形，正方形等都是中心对称图形．
    故答案为：平行四边形，矩形，正方形（答案不唯一）．
    点评：本题属于开放性试题，答案不唯一．主要考查了中心对称图形的定义：如果一个图形绕某一点旋转180°后能够与自身重合，那么这个图形就叫做中心对称图形，这个点叫做对称中心．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    26、已知：如图，抛物线C1，C2关于x轴对称；抛物线C1，C3关于y轴对称．抛物线C1，C2，C3与x轴相交于A、B、C、D四点；与y相交于E、F两点；H、G、M分别为抛物线C1，C2，C3的顶点．HN垂直于x轴，垂足为N，且|OE|＞|HN|，|AB|≠|HG|
    （1）A、B、C、D、E、F、G、H、M9个点中，四个点可以连接成一个四边形，请你用字母写出下列特殊四边形：菱形
    AHBG
    ；等腰梯形
    HGEF
    ；平行四边形
    EGFM
    ；梯形
    DMHC
    ；（每种特殊四边形只能写一个，写错、多写记0分）
    （2）证明其中任意一个特殊四边形；
    （3）写出你证明的特殊四边形的性质．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2012•毕节地区）如图①，有一张矩形纸片，将它沿对角线AC剪开，得到△ACD和△A′BC′．
    （1）如图②，将△ACD沿A′C′边向上平移，使点A与点C′重合，连接A′D和BC，四边形A′BCD是
    平行四边
    平行四边
    形；
    （2）如图③，将△ACD的顶点A与A′点重合，然后绕点A沿逆时针方向旋转，使点D、A、B在同一直线上，则旋转角为
    90
    90
    度；连接CC′，四边形CDBC′是
    直角梯
    直角梯
    形；
    （3）如图④，将AC边与A′C′边重合，并使顶点B和D在AC边的同一侧，设AB、CD相交于E，连接BD，四边形ADBC是什么特殊四边形？请说明你的理由．

    查看答案和解析>>

    科目：初中数学 来源：同步训练与评价·数学·八年级·上 题型：013

    已知四边形ABCD中，AC与BD交于O，如果只给出条件“AB∥CD”，那么还不能判定四边形ABCD为平行四边形，给出以下4种说法：

    ①如果再加上条件“BC＝AD”，那么四边形一定是平行四边形

    ②如果再加上条件“∠BAD＝∠BCD”，那么四边形一定是平行四边形

    ③如果再加上条件“AO＝CO”，那么四边形一定是平行四边形

    ④如果再加上条件“∠DBA＝∠CAB”，那么四边形一定是平行四边形

    其中正确的说法是

    [　　]

    A．①和②
    B．①、③和④
    C．②和③
    D．②、③和④

    查看答案和解析>>

    科目：初中数学 来源：伴你学数学课　　九年级上 题型：022

    在四边形ABCD中，AB∥CD，AC与BD相交于点O．下面有六种说法：

    (1)如果再加上条件“AD∥BC”，那么四边形ABCD一定是平行四边形；

    (2)如果再加上条件“AB＝CD”，那么四边形ABCD一定是平行四边形；

    (3)如果再加上条件“∠DAB＝∠DCB”，那么四边形ABCD一定是平行四边形；

    (4)如果再加上条件“BC＝AD”，那么四边形ABCD一定是平行四边形；

    (5)如果再加上条件“AO＝CO”，那么四边形ABCD一定是平行四边形；

    (6)如果再加上条件“∠DAC＝∠CAB”，那么四边形ABCD一定是平行四边形．

    其中正确的说法有________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    观察探究，完成说明和填空．

        如图①，在四边形ABCD中，点E、F、G、H分别是边AB、BC、CD、DA的中点，顺次连接点E、F、G、H，得到的四边形．EFGH叫做中点四边形．

        (1)试说明四边形EFGH是平行四边形；

        (2)如图②，当四边形ABCD变成等腰梯形时，它的中点四边形是菱形，请你探究并填空：

        当四边形ABCD变成平行四边形时，它的中点四边形是_________；

        当四边形ABCD变成矩形时，它的中点四边形是_________；

        当四边形ABCD变成菱形时，它的中点四边形是_________；

        当四边形ABCD变成正方形时，它的中点四边形是_________．

        (3)根据以上观察探究，请你总结中点四边形的形状由原四边形的什么决定的?

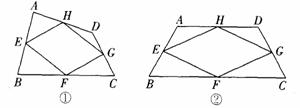
    查看答案和解析>>

    同步练习册答案