
【题目】矩形ABCD中,E是AD的中点,将△ABE折叠后得到△GBE,BG延长交DC于点F,CF=1,FD=2,则BC的长为 .

【答案】2![]() .
.
【解析】
试题此题考查了矩形的判定与性质、折叠的性质、三角形中位线的性质以及全等三角形的判定与性质.此题难度适中,注意辅助线的作法,注意数形结合思想的应用.首先过点E作EM⊥BC于M,交BF于N,易证得△ENG≌△BNM(AAS),MN是△BCF的中位线,根据全等三角形的性质,即可求得GN=MN,由折叠的性质,可得BG=3,继而求得BF的值,又由勾股定理,即可求得BC的长.
解:过点E作EM⊥BC于M,交BF于N,
∵四边形ABCD是矩形,
∴∠A=∠ABC=90°,AD=BC,
∵∠EMB=90°,
∴四边形ABME是矩形,
∴AE=BM,
由折叠的性质得:AE=GE,∠EGN=∠A=90°,
∴EG=BM,
在△ENG和△BNM中
∵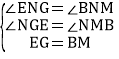 ,
,
∴△ENG≌△BNM(AAS),
∴NG=NM,
∴CM=DE,
∵E是AD的中点,
∴AE=ED=BM=CM,
∵EM∥CD,
∴BN:NF=BM:CM,
∴BN=NF,
∴NM=![]() CF=
CF=![]() ,
,
∴NG=![]() ,
,
∵BG=AB=CD=CF+DF=3,
∴BN=BG-NG=3-![]() =
=![]() ,
,
∴BF=2BN=5,
∴BC=BF2CF2=![]() =2
=2![]() .
.
故答案为:2![]() .
.


科目:初中数学 来源: 题型:
【题目】如图所示,长方形纸片ABCD的长AD=9cm,宽AB=3cm,将其折叠,使点D与点B重合.
求:(1)折叠后DE的长;(2)以折痕EF为边的正方形面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)某园林部门决定利用现有的349盆甲种花卉和295盆乙种花卉搭配A、B两种园艺造型共50个,摆放在迎宾大道两侧.已知搭配一个A种造型需甲种花卉8盆,乙种花卉4盆;搭配一个B种造型需甲种花卉5盆,乙种花卉9盆.
(l)某校2015届九年级某班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种?请你帮助设计出来;
(2)若搭配一个A种造型的成本是200元,搭配一个B种造型的成本是360元,试说明(1)中哪种方案成本最低,最低成本是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点C在AOB的一边OA上,过点C的直线DE//OB,CF平分ACD,CG CF于C .
(1)若O =40,求ECF的度数;
(2)求证:CG平分OCD;
(3)当O为多少度时,CD平分OCF,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,矩形ABCD中,AB=8,AD=6,点E、F分别在边CD、AB上.

(1)若DE=BF,求证:四边形AFCE是平行四边形;
(2)若四边形AFCE是菱形,求菱形AFCE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:k为正数,直线l1:y=kx+k-1与直线l2:y=(k+1)x+k及x轴围成的三角形的面积为Sk,则S1+S2+S3+....+S2016的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
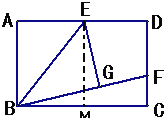
【题目】如图所示,图中的小方格都是边长为1的正方形,![]() 与
与 ![]() 是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
![]() 画出位似中心点O;
画出位似中心点O;
![]() 直接写出
直接写出![]() 与
与![]() 的位似比;
的位似比;
![]() 以位似中心O为坐标原点,以格线所在直线为坐标轴建立平面直角坐标系,并直接写出
以位似中心O为坐标原点,以格线所在直线为坐标轴建立平面直角坐标系,并直接写出![]() 各顶点的坐标.
各顶点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形内角和定理告诉我们:三角形三个内角的和等于180°.如何证明这个定理呢?
我们知道,平角是180°,要证明这个定理就是把三角形的三个内角转移到一个平角中去,请根据如下条件,证明定理.
(定理证明)
已知:△ABC(如图①).
求证:∠A+∠B+∠C=180°.
(定理推论)如图②,在△ABC中,有∠A+∠B+∠ACB=180°,点D是BC延长线上一点,由平角的定义可得∠ACD+∠ACB=180°,所以∠ACD= .从而得到三角形内角和定理的推论:三角形的外角等于与它不相邻的两个内角的和.
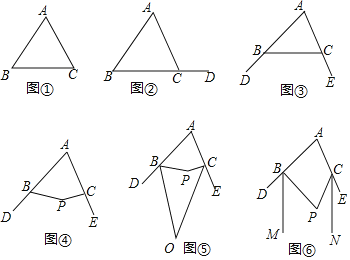
(初步运用)如图③,点D、E分别是△ABC的边AB、AC延长线上一点.
(1)若∠A=80°,∠DBC=150°,则∠ACB= ;
(2)若∠A=80°,则∠DBC+∠ECB= .
(拓展延伸)如图④,点D、E分别是四边形ABPC的边AB、AC延长线上一点.
(1)若∠A=80°,∠P=150°,则∠DBP+∠ECP= ;
(2)分别作∠DBP和∠ECP的平分线,交于点O,如图⑤,若∠O=50°,则∠A和∠P的数量关系为 ;
(3)分别作∠DBP和∠ECP的平分线BM、CN,如图⑥,若∠A=∠P,求证:BM∥CN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 平分
平分![]() 交
交![]() 于点
于点![]() 是
是![]() 上的一点(不与点
上的一点(不与点![]() 重合),
重合),![]() 于点
于点![]() .
.
(1)若![]() ,如图1,当点
,如图1,当点![]() 与点
与点![]() 重合时,求
重合时,求![]() 的度数;
的度数;

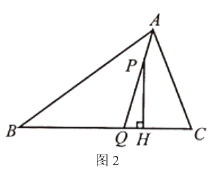
(2)当![]() 是锐角三角形时,如图2,试探索
是锐角三角形时,如图2,试探索![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com