
【题目】已知:k为正数,直线l1:y=kx+k-1与直线l2:y=(k+1)x+k及x轴围成的三角形的面积为Sk,则S1+S2+S3+....+S2016的值为______.
【答案】![]()
【解析】
利用一次函数图象上点的坐标特征可求出两直线与x轴的交点坐标,进而可得出两点间的距离,联立两直线解析式成方程组,通过解方程组可求出两直线的交点坐标,然后根据三角形的面积公式计算S1+S2+S3+....+S2016即可.
解:对直线l1:y=kx+k-1,当y=0时,有kx+k-1=0,解得:![]() ,
,
∴直线l1与x轴的交点坐标为(![]() ,0),
,0),
同理可得出:直线l2与x轴的交点坐标为(![]() ,0),
,0),
∴两直线与x轴交点间的距离![]() .
.
联立直线l1、l2成方程组,得:
![]() ,解得:
,解得:![]() ,
,
∴直线l1、l2的交点坐标为(-1,-1).
∴S1+S2+S3+....+S2016=![]() +
+![]() +
+![]() +……+
+……+![]()
=![]()
=![]()
=![]()
=![]()
=![]() .
.
故答案为:![]() .
.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】用列表法画二次函数![]() 的图象时先列一个表,当表中对自变量x的值以相等间隔的值增加时,函数y所对应的值依次为:20、56、110、182、274、380、506、650,其中有一个值不正确,这个不正确的值是( )
的图象时先列一个表,当表中对自变量x的值以相等间隔的值增加时,函数y所对应的值依次为:20、56、110、182、274、380、506、650,其中有一个值不正确,这个不正确的值是( )
A. 506 B. 380 C. 274 D. 182
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,PB与CD交于点F,∠PBC=∠C.
(1)求证:CB∥PD;
(2)若∠PBC=22.5°,⊙O的半径R=2,求劣弧AC的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
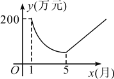
【题目】保护生态环境,建设绿色社会已经从理念变为人们的行动,某化工厂2014年1月的利润为200万元.设2014年1月为第1个月,第x个月的利润为y万元.由于排污超标,该厂决定从2014年1月底起适当限产,并投入资金进行治污改造,导致月利润明显下降,从1月到5月,y与x成反比例,到5月底,治污改造工程顺利完工,从这时起,该厂每月的利润比前一个月增加20万元(如图).
(1)分别求该化工厂治污期间及治污改造工程完工后,y与x之间的函数关系式;
(2)治污改造工程顺利完工后经过几个月,该厂月利润才能达到200万元?
(3)当月利润少于100万元时,为该厂资金紧张期,问该厂资金紧张期共有几个月?
查看答案和解析>>
科目:初中数学 来源: 题型:
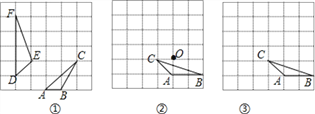
【题目】如图,在![]() 的正方形方格中,每个小正方形的边长都为1,顶点都在网格线交点处的三角形,
的正方形方格中,每个小正方形的边长都为1,顶点都在网格线交点处的三角形, ![]() 是一个格点三角形.
是一个格点三角形.
![]() 在图
在图![]() 中,请判断
中,请判断![]() 与
与![]() 是否相似,并说明理由;
是否相似,并说明理由;
![]() 在图
在图![]() 中,以O为位似中心,再画一个格点三角形,使它与
中,以O为位似中心,再画一个格点三角形,使它与![]() 的位似比为2:1
的位似比为2:1
![]() 在图
在图![]() 中,请画出所有满足条件的格点三角形,它与
中,请画出所有满足条件的格点三角形,它与![]() 相似,且有一条公共边和一个公共角.
相似,且有一条公共边和一个公共角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我校举行的小科技创新发明比赛中,共有60人获奖,组委会原计划按照一等奖5人,二等奖15人,三等奖40人进行奖励.后来经学校研究决定,在该项奖励总奖金不变的情况下,各等级获奖人数实际调整为:一等奖10人,二等奖20人,三等奖30人,调整后一等奖每人奖金降低80元,二等奖每人奖金降低50元,三等奖每人奖金降低30元,调整前二等奖每人奖金比三等奖每人奖金多70元,则调整后一等奖每人奖金比二等奖每人奖金多____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt![]() 中,
中,![]() ,AB=BC,F为AB上一点,连接CF,过B作BH⊥CF于G,交AC于H.
,AB=BC,F为AB上一点,连接CF,过B作BH⊥CF于G,交AC于H.
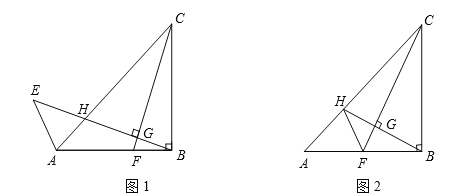
(1)如图1,延长GH到点E,使GE=GC,连接AE,求![]() 的度数;
的度数;
(2)如图2,若F为AB中点,连接FH,请探究BH、FH、CF的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一节前夕,某商店从厂家购进![]() 两种礼盒,已知
两种礼盒,已知![]() 两种礼盒的单价比为
两种礼盒的单价比为![]() ,单价和为
,单价和为![]() 元
元
(1)求![]() 两种礼盒的单价分别是多少元?
两种礼盒的单价分别是多少元?
(2)该商店购进这两种礼盒恰好用去![]() 元,且购进
元,且购进![]() 种礼盒最多
种礼盒最多![]() 个,
个,![]() 种礼盒的数量不超过
种礼盒的数量不超过![]() 种礼盒数量的
种礼盒数量的![]() 倍,共有哪几种进货方案?
倍,共有哪几种进货方案?
(3)根据市场行情,销售一个![]() 种礼盒可获利
种礼盒可获利![]() 元,销售一个
元,销售一个![]() 种礼盒可获利
种礼盒可获利![]() 元.为奉献爱心,该商店决定每售出一个
元.为奉献爱心,该商店决定每售出一个![]() 种礼盒,为爱心公益基金捐款
种礼盒,为爱心公益基金捐款![]() 元,每个
元,每个![]() 种礼盒的利润不变,在(2)的条件下,要使礼盒全部售出后所有方案获利相同,
种礼盒的利润不变,在(2)的条件下,要使礼盒全部售出后所有方案获利相同,![]() 的值是多少?此时该商店可获利多少元?
的值是多少?此时该商店可获利多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com