
 如图,AB是半圆O的直径,CD⊥AB于点C,交半圆于点E,DF切半圆于点F.已知∠AEF=135°.
如图,AB是半圆O的直径,CD⊥AB于点C,交半圆于点E,DF切半圆于点F.已知∠AEF=135°.分析 (1)证明:连接OF,根据圆内接四边形的性质得到∠AEF+∠B=180°,由于∠AEF=135°,得出∠B=45°,于是得到∠AOF=2∠B=90°,由DF切⊙O于F,得到∠DFO=90°,由于DC⊥AB,得到∠DCO=90°,于是结论可得;
(2)过E作EM⊥BF于M,由四边形DCOF是矩形,得到OF=DC=OA,由于OC=CE,推出AC=DE,设DE=x,则AC=x,在Rt△FOB中,∠FOB=90°,OF=OB,BF=2$\sqrt{2}$,由勾股定理得:OF=OB=2,则AB=4,BC=4-x,由于AC=DE,OCDF=CE,由勾股定理得:AE=EF,通过Rt△ECA≌Rt△EMF,得出AC=MF=DE=x,在Rt△ECB和Rt△EMB中,由勾股定理得:BC=BM,问题可得.
解答 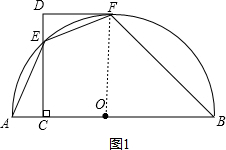 (1)证明:连接OF,
(1)证明:连接OF,
∵A、E、F、B四点共圆,
∴∠AEF+∠B=180°,
∵∠AEF=135°,
∴∠B=45°,
∴∠AOF=2∠B=90°,
∵DF切⊙O于F,
∴∠DFO=90°,
∵DC⊥AB,
∴∠DCO=90°,
即∠DCO=∠FOC=∠DFO=90°,
∴四边形DCOF是矩形,
∴DF∥AB;
(2)解: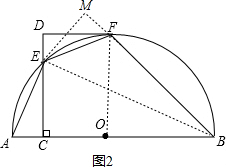 过E作EM⊥BF于M,
过E作EM⊥BF于M,
∵四边形DCOF是矩形,
∴OF=DC=OA,
∵OC=CE,
∴AC=DE,
设DE=x,则AC=x,
∵在Rt△FOB中,∠FOB=90°,OF=OB,BF=2$\sqrt{2}$,由勾股定理得:OF=OB=2,
则AB=4,BC=4-x,
∵AC=DE,OCDF=CE,
∴由勾股定理得:AE=EF,
∴∠ABE=∠FBE,
∵EC⊥AB,EM⊥BF
∴EC=EM,∠ECB=∠M=90°,
在Rt△ECA和Rt△EMF中
$\left\{\begin{array}{l}{AE=EF}\\{EC=EM}\end{array}\right.$
∴Rt△ECA≌Rt△EMF,
∴AC=MF=DE=x,
在Rt△ECB和Rt△EMB中,由勾股定理得:BC=BM,
∴BF=BM-MF=BC-MF=4-x-x=2$\sqrt{2}$,
解得:x=2-$\sqrt{2}$,
即DE=2-$\sqrt{2}$.
点评 本题考查了圆周角性质,圆内接四边形的性质,全等三角形的性质和判定,角平分线性质,矩形的性质和判定的应用,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
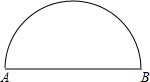 小军在为班级办黑板报时遇到了一个难题,在版面设计过程中需将一个半圆面三等分,请你帮助他设计一个合理的等分方案.(要求:不写作法,保留作图痕迹,写出结论.)
小军在为班级办黑板报时遇到了一个难题,在版面设计过程中需将一个半圆面三等分,请你帮助他设计一个合理的等分方案.(要求:不写作法,保留作图痕迹,写出结论.)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
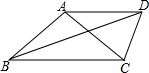 如图,等腰△ABC中,AB=AC,∠BAC=100°,BD平分∠ABC,AD∥BC,连接CD,则∠ADC的度数为( )
如图,等腰△ABC中,AB=AC,∠BAC=100°,BD平分∠ABC,AD∥BC,连接CD,则∠ADC的度数为( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某企业接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元,为按时完成任务,该企业招收了新工人,设新工人李明第x天生产的粽子数量为y只,y与x满足下列关系式:
某企业接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元,为按时完成任务,该企业招收了新工人,设新工人李明第x天生产的粽子数量为y只,y与x满足下列关系式:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com