
解:(1)如图①,过点C作CE⊥AB,垂足为E.
在Rt△ACE中,AC=5

,∠CAB=45°,
∴AE=CE=AC•sin45°=

.
∴BE=AB-AE=17-5=12,

.
∴tanB=

.
∵CB切⊙O于点D,
∴OD⊥BC.
又

=tanB=

,
∴BD=
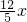
.
∵S
四边形AODC=S
△ABC-S
△BOD,
∴

-

=

=

;
(2)过点C作CF⊥CB交AB于F.
在Rt△BCF中,CF=BC•tanB=13×

=

.
∴x的取值范围是0<x≤

.
说明:答案为0<x<

不扣分;

(3)当⊙O与BC、AC都相切时,
设⊙O与AC的切点为G,连接OG、OC(如图②),则OG=OD=x.
∵S
△AOC+S
△BOC=S
△ABC,
∴

.
∴

.
分析:(1)根据题目条件和切线的性质,建立起半径和BD的关系式,然后根据四边形面积公式和三角形面积公式得出S
四边形AODC=S
△ABC-S
△BOD,得出y与x的函数关系式;
(2)结合图形,易得当O在B点时,圆的半径最小,O在C点时,圆的半径最大,求出CF的长即可;
(3)当⊙O与BC、AC都相切时,利用S
△AOC+S
△BOC=S
△ABC,即可求出x的值.
点评:此题考查了利用图形之间的关系建立函数关系式的能力,解答此类题目的关键是将面积之间的关系作为桥梁,要熟知各种图形的面积公式.

 ,∠CAB=45°,点O在BA上移动,以O为圆心作⊙O,
,∠CAB=45°,点O在BA上移动,以O为圆心作⊙O, 使⊙O与边BC相切,切点为D,设⊙O的半径为x,四边形AODC的面积为y.
使⊙O与边BC相切,切点为D,设⊙O的半径为x,四边形AODC的面积为y. 解:(1)如图①,过点C作CE⊥AB,垂足为E.
解:(1)如图①,过点C作CE⊥AB,垂足为E. ,∠CAB=45°,
,∠CAB=45°, .
. .
. .
. =tanB=
=tanB= ,
,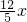 .
. -
- =
= =
= ;
; =
= .
. .
. 不扣分;
不扣分;
 .
. .
.

 ABC考王全优卷系列答案
ABC考王全优卷系列答案 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为