
【题目】如图,在四边形ABCD中,BC、AD不平行,且∠BAD+∠ADC=270°,E、F分别是AD、BC的中点,已知EF=4,求AB2+CD2的值.
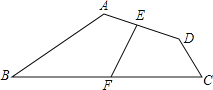
【答案】AB2+CD2=64.
【解析】
试题分析:连接BD,取BD的中点M,连接EM并延长交BC于N,连接FM,根据三角形中位线定理得到EM=![]() AB,FM=
AB,FM=![]() CD,∠NMF=90°,根据勾股定理计算即可.
CD,∠NMF=90°,根据勾股定理计算即可.
解:连接BD,取BD的中点M,连接EM并延长交BC于N,连接FM,
∵∠BAD+∠ADC=270°,
∴∠ABC+∠C=90°,
∵E、F、M分别是AD、BC、BD的中点,
∴EM∥AB,FM∥CD,EM=![]() AB,FM=
AB,FM=![]() CD,
CD,
∴∠MNF=∠ABC,∠MFN=∠C,
∴∠MNF+∠MFN=90°,即∠NMF=90°,
由勾股定理得,ME2+MF2=EF2=16,
∴AB2+CD2=(2ME)2+(2MF)2=64.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
【题目】
![]()
(1)请你根据图中A、B两点的位置,分别写出它们所表示的有理数
A: _________ B: _________ ;
(2)观察数轴,与点A的距离为4的点表示的数是:__________ ;
(3)若将数轴折叠,使得A点与-3表示的点重合,则B点与数____表示的点重合;
(4)若数轴上M、N两点之间的距离为2016(M在N的左侧),且M、N两点经过(3)中折叠后互相重合,则M、N两点表示的数分别是:
M: N: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给定一组数据,下列说法正确的是( )
A. 这组数据的平均数是其中一个数据 B. 这组数据的中位数只有一个
C. 这组数据的众数只有一个 D. 这组数据不可能没有众数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中正确的是( )
A. 有两条边相等的两个等腰三角形全等
B. 两腰对应相等的两个等腰三角形全等
C. 两角对应相等的两个等腰三角形全等
D. 一边对应相等的两个等边三角形全等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8cm,BC=20cm,E是AD的中点.动点P从A点出发,沿A-B-C路线以1cm/秒的速度运动,运动的时间为t秒.将![]() APE以EP为折痕折叠,点A的对应点记为M.
APE以EP为折痕折叠,点A的对应点记为M.
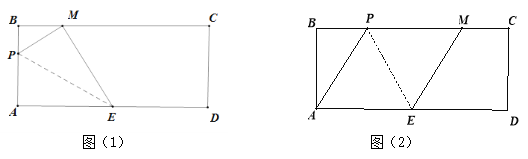
(1) 如图(1),当点P在边AB上,且点M在边BC上时,求运动时间t;
(2) 如图(2),当点P在边BC上,且点M也在边BC上时,求运动时间t;
(3) 直接写出点P在运动过程中线段BM长的最小值 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com