
【题目】我们知道![]() ,于是我们说:“
,于是我们说:“![]() 的整数部分为
的整数部分为![]() ,小数部分则可记为
,小数部分则可记为![]() ”.则:
”.则:
(1)![]() 的整数部分为________,小数部分则可记为________;
的整数部分为________,小数部分则可记为________;
(2)已知![]() 的小数部分为
的小数部分为![]() ,
,![]() 的小数部分为
的小数部分为![]() ,那么
,那么![]() 的值是________;
的值是________;
(3)已知![]() 是
是![]() 的整数部分,
的整数部分,![]() 是
是![]() 的小数部分,求
的小数部分,求![]() 的平方根.
的平方根.
【答案】(1)-1,![]() -2;(2)1;(3)±3.
-2;(2)1;(3)±3.
【解析】
(1)先估算出![]() -3的取值范围,进而可得出结论;
-3的取值范围,进而可得出结论;
(2)估算出3+![]() 与7-
与7-![]() 的取值范围,故可得出a与b的值,代入代数式进行计算即可;
的取值范围,故可得出a与b的值,代入代数式进行计算即可;
(3)先估算出![]() 的取值范围,故可得出x、y的值,代入代数式进行计算即可.
的取值范围,故可得出x、y的值,代入代数式进行计算即可.
(1)∵1<2<4,
∴1<![]() <3,
<3,
∴1-3<![]() -3<0,即-2<
-3<0,即-2<![]() -3<0,
-3<0,
∴![]() -3的整数部分是-1,小数部分是
-3的整数部分是-1,小数部分是![]() -2.
-2.
故答案为:-1,![]() -2;
-2;
(2)∵25<31<36,
∵5<![]() <6,
<6,
∴8<3+![]() <9,
<9,
∴3+![]() 的小数部分是
的小数部分是![]() -5,即a=
-5,即a=![]() -5;
-5;
同理,∵25<31<36,
∵-6<-![]() <-5,
<-5,
∴1<7-![]() <2
<2
∴7-![]() 的小数部分为7-
的小数部分为7-![]() -1=6-
-1=6-![]() ,即b=6-
,即b=6-![]() ,
,
∴a+b=![]() -5+6-
-5+6-![]() =1.
=1.
故答案为:1;
(3)∵9<10<16,
∴3<![]() <4,
<4,
∴![]() 的整数部分是3,小数部分是
的整数部分是3,小数部分是![]() -3,即a=3,y=
-3,即a=3,y=![]() -3,
-3,
∴(y![]() )x1=(
)x1=(![]() -3-
-3-![]() )3-1=(-3)2=9,
)3-1=(-3)2=9,
∵±![]() =±3,
=±3,
∴(y![]() )x1的平方根是±3.
)x1的平方根是±3.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为-7,点B表示的数为5,点C到点A,点B的距离相等,动点P从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动的时间为![]() (
(![]() >0)秒
>0)秒
(1)点C表示的数是_________.
(2)求当![]() 等于多少秒时,点P到达点B处.
等于多少秒时,点P到达点B处.
(3)点P表示的数是_________(用含有![]() 的代数式表示).
的代数式表示).
(4)求当t等于多少秒时,PC之间的距离为2个单位长度(只列式,不计算).
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于O点,且BE=BF,∠BEF=2∠BAC。

(1)求证:OE=OF;
(2)若BC=![]() ,求AB的长。
,求AB的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列单项式:![]() ,
,![]() ,
,![]() ,
,![]() ,…
,…![]() ,
,![]() ,…写出第
,…写出第![]() 个单项式,为了解这个问题,特提供下面的解题思路.
个单项式,为了解这个问题,特提供下面的解题思路.
![]() 这组单项式的系数的符号,绝对值规律是什么?
这组单项式的系数的符号,绝对值规律是什么?
![]() 这组单项式的次数的规律是什么?
这组单项式的次数的规律是什么?
![]() 根据上面的归纳,你可以猜想出第
根据上面的归纳,你可以猜想出第![]() 个单项式是什么?
个单项式是什么?
![]() 请你根据猜想,请写出第
请你根据猜想,请写出第![]() 个,第
个,第![]() 个单项式.
个单项式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,若AC=6,BC=8,CD=3.

(1)求DE的长;
(2)求△ADB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,二次函数y=ax2+2ax﹣3a(a≠0)图象的顶点为H,与x轴交于A、B两点(B在A点右侧),点H、B关于直线l: ![]() 对称.
对称. 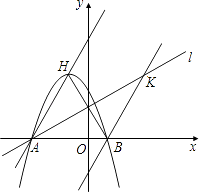
(1)求A、B两点坐标,并证明点A在直线l上;
(2)求二次函数解析式; 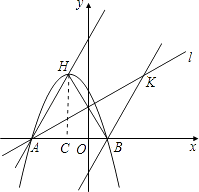
(3)过点B作直线BK∥AH交直线l于K点,M、N分别为直线AH和直线l上的两个动点,连接HN、NM、MK,求HN+NM+MK和的最小值. 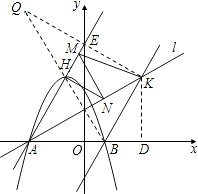
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明去文具用品商店给同学买某品牌水性笔,已知甲、乙两商店都有该品牌的水性笔且标价都是2元/支,但甲、乙两商店的优惠条件却不同.
甲商店:若购买不超过10支,则按标价付款;若一次购10支以上,则超过10支的部分按标价的60%付款. 乙商店:按标价的80%付款.
在水性笔的质量等因素相同的条件下.
(1)设小明要购买的该品牌笔数是x(x>10)支,请用含x的式子分别表示在甲、乙两个商店购买该品牌笔买水性笔的费用.
(2)若小明要购买该品牌笔30支,你认为在甲、乙两商店中,到哪个商店购买比较省钱?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com