解:(1)解法一:2a(a+b)-(a+b)
2=2a
2+2ab-(a
2+2ab+b
2)
=a
2-b
2,
当a=

,b=

时,
原式=(

)
2-(

)
2=-2;
解法二:2a(a+b)-(a+b)
2=(a+b)(2a-a-b)
=(a+b)(a-b)
=a
2-b
2,
当a=

,b=

时,
原式=(

)
2-(

)
2=-2;
(2)根据数轴所示,得-1<a<0<1<b,
∴a+1>0,b-1>0,a-b<0,
∴
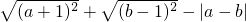
=|a+1|+|b-1|-|a-b|=a+1+b-1+a-b=2a.
分析:(1)首先对代数式进行化简,可以直接根据乘法公式进行计算,亦可借助因式分解法简便计算,再进一步把字母的值代入计算;
(2)先根据数轴所示,得出-1<a<0<1<b,即可推出a+1>0,b-1>0,a-b<0,再根据二次根式的性质及绝对值的定义,即可推出
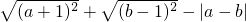
=|a+1|+|b-1|-|a-b|=a+1+b-1+a-b=2a.
点评:本题(1)主要考查单项式乘多项式的法则,完全平方公式,熟记公式和法则是解(1)题的关键.完全平方公式:(a+b)
2=a
2+2ab+b
2;
(2)考查了实数与数轴的对应关系、二次根式的性质与化简.解答此类题目时应先根据由数轴上a,b两点的位置确定a,b的符号及绝对值的大小,再根据二次根式的性质解答即可.

 (1)先化简再求值:2a(a+b)-(a+b)2,其中
(1)先化简再求值:2a(a+b)-(a+b)2,其中 ,
,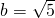 .
.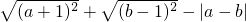 .
. ,b=
,b= 时,
时, )2-(
)2-( )2=-2;
)2=-2; ,b=
,b= 时,
时, )2-(
)2-( )2=-2;
)2=-2;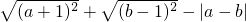 =|a+1|+|b-1|-|a-b|=a+1+b-1+a-b=2a.
=|a+1|+|b-1|-|a-b|=a+1+b-1+a-b=2a.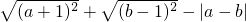 =|a+1|+|b-1|-|a-b|=a+1+b-1+a-b=2a.
=|a+1|+|b-1|-|a-b|=a+1+b-1+a-b=2a.

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案