
【题目】如图,∠MAN=60°,AP平分∠MAN,点B是射线AP上一定点,点C在直线AN上运动,连接BC,将∠ABC(0°<∠ABC<120°)的两边射线BC和BA分别绕点B顺时针旋转120°,旋转后角的两边分别与射线AM交于点D和点E.

(1)如图1,当点C在射线AN上时,
①请判断线段BC与BD的数量关系,直接写出结论;
②请探究线段AC,AD和BE之间的数量关系,写出结论并证明;
(2)如图2,当点C在射线AN的反向延长线上时,BC交射线AM于点F,若AB=4,AC=![]() ,请直接写出线段AD和DF的长.
,请直接写出线段AD和DF的长.
【答案】(1)①BC=BD;②AD+AC=![]() BE;(2)AD=5
BE;(2)AD=5![]() , DF=
, DF=![]() .
.
【解析】试题分析:(1)①结论:BC=BD.只要证明△BGD≌△BHC即可.②结论:AD+AC=![]() BE.只要证明AD+AC=2AG=2EG,再证明EB=
BE.只要证明AD+AC=2AG=2EG,再证明EB=![]() BE即可解决问题;
BE即可解决问题;
(2)如图2中,作BG⊥AM于G,BH⊥AN于H,AK⊥CF于K.由(1)可知,△ABG≌△ABH,△BGD≌△BHC,易知BH,AH,BC,CH, AD的长,由sin∠ACH=![]() ,推出AK的长,设FG=y,则AF=
,推出AK的长,设FG=y,则AF=![]() ﹣y,BF=
﹣y,BF=![]() ,由△AFK∽△BFG,可得
,由△AFK∽△BFG,可得![]() ,可得关于y的方程,求出y即可解决问题.
,可得关于y的方程,求出y即可解决问题.
试题解析:(1)①结论:BC=BD,
理由:如图1中,作BG⊥AM于G,BH⊥AN于H,
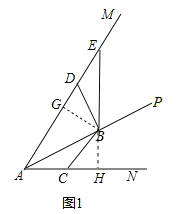
∵∠MAN=60°,PA平分∠MAN,BG⊥AM于G,BH⊥AN于H,∴BG=BH,∠GBH=∠CBD=120°,∴∠CBH=∠GBD,∵∠BGD=∠BHC=90°,∴△BGD≌△BHC,∴BD=BC;
②结论:AD+AC=![]() BE,
BE,
∵∠ABE=120°,∠BAE=30°,∴∠BEA=∠BAE=30°,∴BA=BE,∵BG⊥AE,∴AG=GE,EG=BEcos30°=![]() BE,∵△BGD≌△BHC,∴DG=CH,∵AB=AB,BG=BH,∴Rt△ABG≌Rt△ABH,∴AG=AH,∴AD+AC=AG+DG+AH﹣CH=2AG=
BE,∵△BGD≌△BHC,∴DG=CH,∵AB=AB,BG=BH,∴Rt△ABG≌Rt△ABH,∴AG=AH,∴AD+AC=AG+DG+AH﹣CH=2AG=![]() BE,∴AD+AC=
BE,∴AD+AC=![]() BE;
BE;
(2)如图2中,作BG⊥AM于G,BH⊥AN于H,AK⊥CF于K,
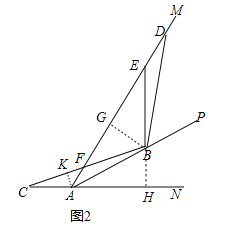
由(1)可知,△ABG≌△ABH,△BGD≌△BHC,
易知BH=GB=2,AH=AG=EG=![]() ,BC=BD=
,BC=BD=![]() =
=![]() ,CH=DG=
,CH=DG=![]() ,
,
∴AD=![]() ,∵sin∠ACH=
,∵sin∠ACH=![]() ,∴
,∴![]() ,∴AK=
,∴AK=![]() ,
,
设FG=y,则AF=![]() ﹣y,BF=
﹣y,BF=![]() ,
,
∵∠AFK=∠BFG,∠AKF=∠BGF=90°,
∴△AFK∽△BFG,∴![]() ,∴
,∴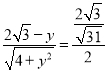 ,解得y=
,解得y=![]() 或
或![]() (舍弃),
(舍弃),
∴DF=GF+DG=![]() ,即DF=
,即DF=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点 A,B的坐标分别为(0,3),(1,0),△ABC是等腰直角三角形,∠ABC=90°.
(1)图1中,点C的坐标为 ;
(2)如图2,点D的坐标为(0,1),点E在射线CD上,过点B 作BF⊥BE交y轴于点F.
①当点E为线段CD的中点时,求点F的坐标;
②当点E在第二象限时,请直接写出F点纵坐标y的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,﹣4),连接AO,AO=5,sin∠AOC=![]() .
.
(1)求反比例函数的解析式;
(2)连接OB,求△AOB的面积.
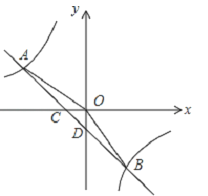
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x上有点A1,A2,A3,…An+1,且OA1=1,A1A2=2,A2A3=4,AnAn+1=2n分别过点A1,A2,A3,…An+1作直线y=
x上有点A1,A2,A3,…An+1,且OA1=1,A1A2=2,A2A3=4,AnAn+1=2n分别过点A1,A2,A3,…An+1作直线y=![]() x的垂线,交y轴于点B1,B2,B3,…Bn+1,依次连接A1B2,A2B3,A3B4,…AnBn+1,得到△A1B1B2,△A2B2B3,△A3B3B4,…,△AnBnBn+1,则△AnBnBn+1的面积为________.(用含有正整数n的式子表示)
x的垂线,交y轴于点B1,B2,B3,…Bn+1,依次连接A1B2,A2B3,A3B4,…AnBn+1,得到△A1B1B2,△A2B2B3,△A3B3B4,…,△AnBnBn+1,则△AnBnBn+1的面积为________.(用含有正整数n的式子表示)
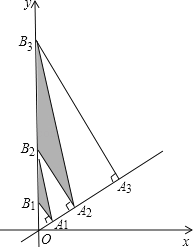
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=3x与双曲线y=![]() (k≠0,且x>0)交于点A,点A的横坐标是1.
(k≠0,且x>0)交于点A,点A的横坐标是1.
(1)求点A的坐标及双曲线的解析式;
(2)点B是双曲线上一点,且点B的纵坐标是1,连接OB,AB,求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2﹣2x+c(a≠0)与x轴、y轴分别交于点A,B,C三点,已知点A(﹣2,0),点C(0,﹣8),点D是抛物线的顶点.
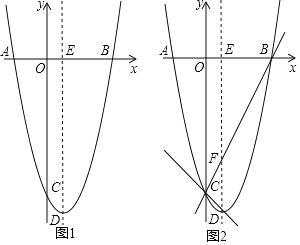
(1)求抛物线的解析式及顶点D的坐标;
(2)如图1,抛物线的对称轴与x轴交于点E,第四象限的抛物线上有一点P,将△EBP沿直线EP折叠,使点B的对应点B'落在抛物线的对称轴上,求点P的坐标;
(3)如图2,设BC交抛物线的对称轴于点F,作直线CD,点M是直线CD上的动点,点N是平面内一点,当以点B,F,M,N为顶点的四边形是菱形时,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3,已知A(1,3),A1(2,3),A2(4,3),A3(8,3),B(2,0),B1(4,0),B2(8,0),B3(16,0).

(1)观察每次变换前后的三角形有何变化,找出规律,按些变换规律将△OA3B3变换成△OA4B4,则A4的坐标是_______,B4的坐标是_________.
(2)若按第(1)题的规律将△OAB进行了n次变换,得到△OAnBn,比较每次变换中三角形顶点坐标有何变化,找出规律,请推测An的坐标是_______,Bn的坐标是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,最合适采用抽样调查的是( )
A.策坐高铁对旅客的行李的检查B.调查七年级一班全体同学的身高情况
C.了解长沙市民对春节晚会节目的满意程度D.对新研发的新型战斗机的零部件进行检查
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com