
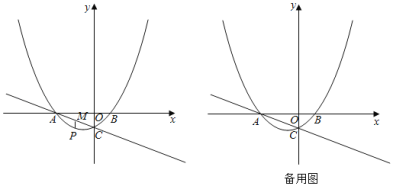
°æƒø°ø»ÁÕº£¨≈◊ŒÔœfl![]() Ωªx÷·”⁄A£¨B¡Ωµ„£¨Ωªy÷·”⁄µ„C£Æ÷±œfl
Ωªx÷·”⁄A£¨B¡Ωµ„£¨Ωªy÷·”⁄µ„C£Æ÷±œfl![]() æ≠π˝µ„A£¨C£Æ
æ≠π˝µ„A£¨C£Æ
£®1£©«Û≈◊ŒÔœflµƒΩ‚Œˆ Ω£ª
£®2£©µ„P «≈◊ŒÔœfl…œ“ª∂ص„£¨π˝µ„P◊˜x÷·µƒ¥πœfl£¨Ωª÷±œflAC”⁄µ„M£¨…˵„Pµƒ∫·◊¯±ÍŒ™m£Æ
¢Ÿµ±![]() «÷±Ω«»˝Ω«–Œ ±£¨«Ûµ„Pµƒ◊¯±Í£ª
«÷±Ω«»˝Ω«–Œ ±£¨«Ûµ„Pµƒ◊¯±Í£ª
¢⁄◊˜µ„Bπÿ”⁄µ„Cµƒ∂‘≥∆µ„![]() £¨‘Ú∆Ω√ʃ⁄¥Ê‘⁄÷±œfll£¨ πµ„M£¨B£¨
£¨‘Ú∆Ω√ʃ⁄¥Ê‘⁄÷±œfll£¨ πµ„M£¨B£¨![]() µΩ∏√÷±œflµƒæ‡¿Î∂ºœ‡µ»£Æµ±µ„P‘⁄y÷·”“≤‡µƒ≈◊ŒÔœfl…œ£¨«“”ε„B≤ª÷ÿ∫œ ±£¨«Î÷±Ω”–¥≥ˆ÷±œfl
µΩ∏√÷±œflµƒæ‡¿Î∂ºœ‡µ»£Æµ±µ„P‘⁄y÷·”“≤‡µƒ≈◊ŒÔœfl…œ£¨«“”ε„B≤ª÷ÿ∫œ ±£¨«Î÷±Ω”–¥≥ˆ÷±œfl![]() µƒΩ‚Œˆ Ω£Æ£®k£¨bø…”√∫¨mµƒ Ω◊”±Ì 棩
µƒΩ‚Œˆ Ω£Æ£®k£¨bø…”√∫¨mµƒ Ω◊”±Ì 棩
°æ¥∞∏°ø£®1£©![]() £®2£©¢Ÿ
£®2£©¢Ÿ![]() ªÚ
ªÚ![]() £¨¢⁄÷±œfllµƒΩ‚Œˆ ΩŒ™
£¨¢⁄÷±œfllµƒΩ‚Œˆ ΩŒ™![]() ,
,![]() ªÚ
ªÚ![]() .
.
°æΩ‚Œˆ°ø
£®1£©¿˚”√“ª¥Œ∫Ø ˝ÕºœÛ…œµ„µƒ◊¯±ÍÃÿ’˜ø…«Û≥ˆµ„A£¨Cµƒ◊¯±Í£¨∏˘æ›µ„A£¨Cµƒ◊¯±Í£¨¿˚”√¥˝∂®œµ ˝∑®ø…«Û≥ˆ∂˛¥Œ∫Ø ˝Ω‚Œˆ Ω£ª
£®2£©¢Ÿ”…PM°Õx÷·ø…µ√≥ˆ°œPMC°Ÿ90°„£¨∑÷°œMPC=90°„º∞°œPCM=90°„¡Ω÷÷«Èøˆøº¬«£∫£®i£©µ±°œMPC=90°„ ±£¨PC°Œx÷·£¨¿˚”√∂˛¥Œ∫Ø ˝ÕºœÛ…œµ„µƒ◊¯±ÍÃÿ’˜ø…«Û≥ˆµ„Pµƒ◊¯±Í£ª£®ii£©µ±°œPCM=90°„ ±£¨…ËPC”Îx÷·Ωª”⁄µ„D£¨“◊÷§°˜AOC°◊°˜COD£¨¿˚”√œ‡À∆»˝Ω«–Œµƒ–‘÷ ø…«Û≥ˆµ„Dµƒ◊¯±Í£¨∏˘æ›µ„C£¨Dµƒ◊¯±Í£¨¿˚”√¥˝∂®œµ ˝∑®ø…«Û≥ˆ÷±œflPCµƒΩ‚Œˆ Ω£¨¡™¡¢÷±œflPC∫Õ≈◊ŒÔœflµƒΩ‚Œˆ Ω≥…∑Ω≥Ã◊È£¨Õ®π˝Ω‚∑Ω≥Ã◊Èø…«Û≥ˆµ„Pµƒ◊¯±Í£Æ◊€…œ£¨¥ÀŒ µ√Ω‚£ª
¢⁄¿˚”√∂˛¥Œ∫Ø ˝ÕºœÛ…œµ„µƒ◊¯±ÍÃÿ’˜º∞“ª¥Œ∫Ø ˝ÕºœÛ…œµ„µƒ◊¯±ÍÃÿ’˜ø…µ√≥ˆµ„B£¨Mµƒ◊¯±Í£¨Ω·∫œµ„Cµƒ◊¯±Íø…µ√≥ˆµ„B°‰µƒ◊¯±Í£¨∏˘æ›µ„M£¨B£¨B°‰µƒ◊¯±Í£¨¿˚”√¥˝∂®œµ ˝∑®ø…∑÷±«Û≥ˆ÷±œflBM£¨B°‰M∫ÕBB°‰µƒΩ‚Œˆ Ω£¨¿˚”√∆Ω––œflµƒ–‘÷ ø…«Û≥ˆ÷±œfllµƒΩ‚Œˆ Ω£Æ
Ω‚£∫£®1£©µ±![]() ±£¨
±£¨![]() £¨
£¨
![]() µ„Cµƒ◊¯±ÍŒ™
µ„Cµƒ◊¯±ÍŒ™![]() £ª
£ª
µ±![]() ±£¨
±£¨![]() £¨
£¨
Ω‚µ√£∫![]() £¨
£¨
![]() µ„Aµƒ◊¯±ÍŒ™
µ„Aµƒ◊¯±ÍŒ™![]() £Æ
£Æ
Ω´![]() £¨
£¨![]() ¥˙»Î
¥˙»Î![]() £¨µ√£∫
£¨µ√£∫
![]() £¨Ω‚µ√£∫
£¨Ω‚µ√£∫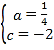 £¨
£¨
![]() ≈◊ŒÔœflµƒΩ‚Œˆ ΩŒ™
≈◊ŒÔœflµƒΩ‚Œˆ ΩŒ™![]() £Æ
£Æ
£®2£©¢Ÿ![]() ÷·£¨
÷·£¨
![]() £¨
£¨
![]() ∑÷¡Ω÷÷«Èøˆøº¬«£¨»ÁÕº1À˘ æ£Æ
∑÷¡Ω÷÷«Èøˆøº¬«£¨»ÁÕº1À˘ æ£Æ
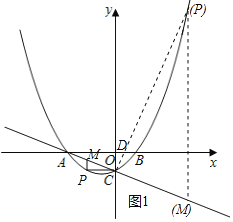
£®i£©µ±![]() ±£¨
±£¨![]() ÷·£¨
÷·£¨
![]() µ„Pµƒ◊›◊¯±ÍŒ™©Å2£Æ
µ„Pµƒ◊›◊¯±ÍŒ™©Å2£Æ
µ±![]() ±£¨
±£¨![]() £¨
£¨
Ω‚µ√£∫![]() £¨
£¨![]() £¨
£¨
![]() µ„Pµƒ◊¯±ÍŒ™
µ„Pµƒ◊¯±ÍŒ™![]() £ª
£ª
£®ii£©µ±![]() ±£¨…ËPC”Îx÷·Ωª”⁄µ„D£Æ
±£¨…ËPC”Îx÷·Ωª”⁄µ„D£Æ
![]() £¨
£¨![]() £¨
£¨
![]() £Æ
£Æ
”÷![]() £¨
£¨
![]() £¨
£¨
![]() £¨º¥
£¨º¥![]() £¨
£¨
![]() £¨
£¨
![]() µ„Dµƒ◊¯±ÍŒ™
µ„Dµƒ◊¯±ÍŒ™![]() £Æ
£Æ
…Ë÷±œflPCµƒΩ‚Œˆ ΩŒ™![]() £¨
£¨
Ω´![]() £¨
£¨![]() ¥˙»Î
¥˙»Î![]() £¨µ√£∫
£¨µ√£∫
![]() £¨Ω‚µ√£∫
£¨Ω‚µ√£∫![]() £¨
£¨
![]() ÷±œflPCµƒΩ‚Œˆ ΩŒ™
÷±œflPCµƒΩ‚Œˆ ΩŒ™![]() £Æ
£Æ
¡™¡¢÷±œflPC∫Õ≈◊ŒÔœflµƒΩ‚Œˆ Ω≥…∑Ω≥Ã◊È£¨µ√£∫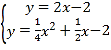 £¨
£¨
Ω‚µ√£∫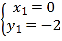 £¨
£¨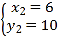 £¨
£¨
µ„Pµƒ◊¯±ÍŒ™![]() £Æ
£Æ
◊€…œÀ˘ ˆ£∫µ±![]() «÷±Ω«»˝Ω«–Œ ±£¨µ„Pµƒ◊¯±ÍŒ™
«÷±Ω«»˝Ω«–Œ ±£¨µ„Pµƒ◊¯±ÍŒ™![]() ªÚ
ªÚ![]() £Æ
£Æ
¢⁄µ±y=0 ±£¨![]() ,
,
Ω‚µ√£∫x1=-4£¨x2=2£¨
°‡µ„Bµƒ◊¯±ÍŒ™£®2£¨0£©£Æ
°flµ„Cµƒ◊¯±ÍŒ™£®0£¨-2£©£¨µ„B£¨B°‰πÿ”⁄µ„C∂‘≥∆£¨
°‡µ„B°‰µƒ◊¯±ÍŒ™£®-2£¨-4£©£Æ
°flµ„Pµƒ∫·◊¯±ÍŒ™m£®m£æ0«“m°Ÿ2£©£¨
°‡µ„Mµƒ◊¯±ÍŒ™![]() ,
,
¿˚”√¥˝∂®œµ ˝∑®ø…«Û≥ˆ£∫÷±œflBMµƒΩ‚Œˆ ΩŒ™![]() £¨÷±œflB°‰MµƒΩ‚Œˆ ΩŒ™
£¨÷±œflB°‰MµƒΩ‚Œˆ ΩŒ™![]() £¨÷±œflBB°‰µƒΩ‚Œˆ ΩŒ™y=x-2£Æ
£¨÷±œflBB°‰µƒΩ‚Œˆ ΩŒ™y=x-2£Æ
∑÷»˝÷÷«Èøˆøº¬«£¨»ÁÕº2À˘ æ£∫
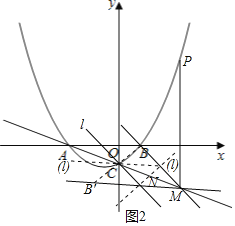
µ±÷±œfll°ŒBM«“π˝µ„C ±£¨÷±œfllµƒΩ‚Œˆ ΩŒ™![]() ,
,
µ±÷±œfll°ŒB°‰M«“π˝µ„C ±£¨÷±œfllµƒΩ‚Œˆ ΩŒ™![]() ,
,
µ±÷±œfll°ŒBB°‰«“π˝œfl∂ŒCMµƒ÷–µ„![]() ±£¨÷±œfllµƒΩ‚Œˆ ΩŒ™
±£¨÷±œfllµƒΩ‚Œˆ ΩŒ™![]() ,
,
◊€…œÀ˘ ˆ£∫÷±œfllµƒΩ‚Œˆ ΩŒ™![]() ,
,![]() ªÚ
ªÚ![]() .
.



| ƒÍº∂ | ∏fl÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏fl“ª | ∏fl“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl∂˛ | ∏fl∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl»˝ | ∏fl»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø–°∂´∏˘æ›—ßœ∞∫Ø ˝µƒæ≠—È£¨∂‘∫Ø ˝![]() µƒÕºœÛ”Ζ‘÷ Ω¯––¡ÀÃΩæø£Æœ¬√Ê «–°∂´µƒÃΩæøπ˝≥㨫Î≤π≥‰ÕÍ’˚£¨≤¢Ω‚戜‡πÿŒ £∫
µƒÕºœÛ”Ζ‘÷ Ω¯––¡ÀÃΩæø£Æœ¬√Ê «–°∂´µƒÃΩæøπ˝≥㨫Î≤π≥‰ÕÍ’˚£¨≤¢Ω‚戜‡πÿŒ £∫
£®1£©∫Ø ˝![]() µƒ◊‘±‰¡øxµƒ»°÷µ∑∂Œß « £ª
µƒ◊‘±‰¡øxµƒ»°÷µ∑∂Œß « £ª
£®2£©œ¬±Ì «y”Îxµƒº∏◊È∂‘”¶÷µ.
x | °≠ |
|
|
| 0 |
| 1 |
| 2 |
| 3 | 4 | °≠ |
y | °≠ |
|
|
| 2 |
| 4 |
| 2 |
|
| m | °≠ |
±Ì÷–mµƒ÷µŒ™________________£ª
£®3£©»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨√Ë≥ˆ¡À“‘…œ±Ì÷–∏˜∂‘∂‘”¶÷µŒ™◊¯±Íµƒµ„. ∏˘æ›√Ë≥ˆµƒµ„£¨ª≠≥ˆ∫Ø ˝![]() µƒ¥Û÷¬ÕºœÛ£ª
µƒ¥Û÷¬ÕºœÛ£ª
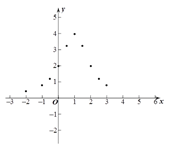
£®4£©Ω·∫œ∫Ø ˝ÕºœÛ£¨«Î–¥≥ˆ∫Ø ˝![]() µƒ“ªÃı–‘÷ £∫______________________.
µƒ“ªÃı–‘÷ £∫______________________.
£®5£©Ω‚戌 £∫»Áπ˚∫Ø ˝![]() ”Î÷±œfly=aµƒΩªµ„”–2∏ˆ£¨ƒ«√¥aµƒ»°÷µ∑∂Œß «______________ .
”Î÷±œfly=aµƒΩªµ„”–2∏ˆ£¨ƒ«√¥aµƒ»°÷µ∑∂Œß «______________ .
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄ABCD÷–£¨AB£Ω6£¨AD£Ω9£¨°œBADµƒ∆Ω∑÷œflΩªBC”⁄µ„E£¨ΩªDCµƒ—”≥§œfl”⁄µ„F£¨BG°ÕAE£¨¥π◊„Œ™G£¨BG£Ω4![]() £¨‘Ú°˜CEFµƒ÷‹≥§Œ™£®°°°°£©
£¨‘Ú°˜CEFµƒ÷‹≥§Œ™£®°°°°£©
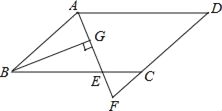
A.11.5B.10C.9.5D.8
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘ƒ∂¡≤ƒ¡œ£∫∏˜¿‡∑Ω≥õƒΩ‚∑®
«ÛΩ‚“ª‘™“ª¥Œ∑Ω≥ã¨∏˘æ›µ» Ωµƒª˘±æ–‘÷ £¨∞—∑Ω≥Ã◊™ªØŒ™x=aµƒ–Œ Ω£Æ«ÛΩ‚∂˛‘™“ª¥Œ∑Ω≥Ã◊È£¨∞—À¸◊™ªØŒ™“ª‘™“ª¥Œ∑Ω≥ÿ¥Ω‚£ª¿‡À∆µƒ£¨«ÛΩ‚»˝‘™“ª¥Œ∑Ω≥Ã◊È£¨∞—À¸◊™ªØŒ™Ω‚∂˛‘™“ª¥Œ∑Ω≥Ã◊ȣƫÛΩ‚“ª‘™∂˛¥Œ∑Ω≥ã¨∞—À¸◊™ªØŒ™¡Ω∏ˆ“ª‘™“ª¥Œ∑Ω≥ÿ¥Ω‚£Æ«ÛΩ‚∑÷ Ω∑Ω≥ã¨∞—À¸◊™ªØŒ™’˚ Ω∑Ω≥ÿ¥Ω‚£¨”…”⁄°∞»•∑÷ƒ∏°±ø…ƒ‹≤˙…˙‘ˆ∏˘£¨À˘“‘Ω‚∑÷ Ω∑Ω≥ñÿ–κϗȣÆ∏˜¿‡∑Ω≥õƒΩ‚∑®≤ªæ°œ‡Õ¨£¨µ´ «À¸√«”–“ª∏ˆπ≤Õ¨µƒª˘±æ ˝—ßÀºœÎ![]() ◊™ªØ£¨∞—Œ¥÷™◊™ªØŒ™“—÷™£Æ
◊™ªØ£¨∞—Œ¥÷™◊™ªØŒ™“—÷™£Æ
”√°∞◊™ªØ°±µƒ ˝—ßÀºœÎ£¨Œ“√«ªπø…“‘Ω‚“ª–©–¬µƒ∑Ω≥ãƿ˝»Á£¨“ª‘™»˝¥Œ∑Ω≥Ãx3+x2-2x=0£¨ø…“‘Õ®π˝“Ú Ω∑÷Ω‚∞—À¸◊™ªØŒ™x(x2+x-2)=0£¨Ω‚∑Ω≥Ãx=0∫Õx2+x-2=0£¨ø…µ√∑Ω≥Ãx3+x2-2x=0µƒΩ‚£Æ
£®1£©Œ £∫∑Ω≥Ãx3+x2-2x=0µƒΩ‚ «x1=0,x2= £¨x3= £ª
£®2£©Õÿ’π£∫”√°∞◊™ªØ°±ÀºœÎ«Û∑Ω≥Ã![]() µƒΩ‚£ª
µƒΩ‚£ª
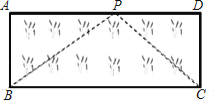
£®3£©”¶”√£∫»ÁÕº£¨“—÷™æÿ–Œ≤›∆∫ABCDµƒ≥§AD=8m£¨øÌAB=3m£¨–°ª™∞—“ª∏˘≥§Œ™10mµƒ…˛◊”µƒ“ª∂ÀπÃ∂®‘⁄µ„B£¨—ÿ≤›∆∫±fl—ÿBA£¨AD◊flµΩµ„P¥¶£¨∞—≥§…˛PB∂Œ¿≠÷±≤¢πÃ∂®‘⁄µ„P£¨»ª∫Û—ÿ≤›∆∫±fl—ÿPD°¢DC◊flµΩµ„C¥¶£¨∞—≥§…˛ £œ¬µƒ“ª∂Œ¿≠÷±£¨≥§…˛µƒ¡Ì“ª∂À«°∫√¬‰‘⁄µ„C£Æ«ÛAPµƒ≥§£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨“—÷™AB£Ω8£¨PŒ™œfl∂ŒAB…œ“ª∏ˆ∂ص„£¨∑÷±“‘AP£¨PBŒ™±fl‘⁄ABµƒÕ¨≤‡◊˜¡‚–ŒAPCD∫ÕPBFE£¨µ„P£¨C£¨E‘⁄“ªÃı÷±œfl…œ£¨°œDAP£Ω60°„£¨M£¨N∑÷± «∂‘Ω«œflAC£¨BEµƒ÷–µ„£¨µ±µ„P‘⁄œfl∂ŒAB…œ“∆∂Ø ±£¨µ„M£¨N÷ƺ‰µƒæ‡¿Î◊Ó∂ÃŒ™£® £©
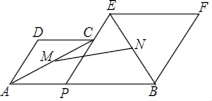
A. ![]() B.
B. ![]() C. 4D. 3
C. 4D. 3
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™æÿ–Œ![]() µƒ“ªÃı±fl
µƒ“ªÃı±fl![]() £¨Ω´æÿ–Œ
£¨Ω´æÿ–Œ![]() ’€µ˛£¨ πµ√∂•µ„
’€µ˛£¨ πµ√∂•µ„![]() ¬‰‘⁄
¬‰‘⁄![]() ±fl…œµƒ
±fl…œµƒ![]() µ„¥¶. »ÁÕº£¨“—÷™’€∫€”αfl
µ„¥¶. »ÁÕº£¨“—÷™’€∫€”αfl![]() Ωª”⁄µ„
Ωª”⁄µ„![]() £¨¡¨Ω·
£¨¡¨Ω·![]() .
.
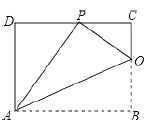
£®1£©«Û÷§£∫![]() £ª
£ª
£®2£©»Ù![]() £¨«Û±fl
£¨«Û±fl![]() µƒ≥§.
µƒ≥§.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø–°¿Óº› ª–°∆˚≥µ‘»ÀŸµÿ¥”Aµÿ–– ªµΩBµÿ£¨–– ª¿Ô≥ÃŒ™360«ß√◊£¨…Ë–°∆˚≥µµƒ–– ª ±º‰Œ™t(µ•Œª£∫–° ±)£¨–– ªÀŸ∂»Œ™v(µ•Œª£∫«ß√◊/–° ±)£¨«“»´≥ÃÀŸ∂»œfi∂®Œ™≤ª≥¨π˝120«ß√◊/–° ±.
£®1£©«Ûvπÿ”⁄tµƒ∫Ø ˝±Ì¥Ô Ω£®≤ª”√–¥»°÷µ∑∂Œß£©£ª
£®2£©–°¿Ó…œŒÁ8µ„º› ª–°∆˚≥µ¥”Aµÿ≥ˆ∑¢.
¢Ÿ–°¿Ó–Ë‘⁄µ±ÃÏ12µ„÷¡13µ„º‰µΩ¥ÔBµÿ£¨«Û–°∆˚≥µ–– ªÀŸ∂»vµƒ∑∂Œß.
¢⁄–°¿Óƒ‹∑Ò‘⁄µ±ÃÏ11µ„30∑÷«∞µΩ¥ÔBµÿ£øÀµ√˜¿Ì”….
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∂˛¥Œ∫Ø ˝µƒÕºœÛæ≠π˝£®©Å1£¨0£©£¨£®3£¨0£©£¨£®1£¨©Å5£©»˝µ„£Æ
£®1£©«Û∏√∂˛¥Œ∫Ø ˝µƒΩ‚Œˆ Ω£ª
£®2£©«Û∏√ÕºœÛµƒ∂•µ„◊¯±Í£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨¿˚”√“ª√Ê«Ω£®«Ωµƒ≥§∂»≤ª≥¨π˝45m£©£¨”√80m≥§µƒ¿È∞ Œß“ª∏ˆæÿ–Œ≥°µÿ£Æ

£®1£©‘ı—˘Œß≤≈ƒ‹ πæÿ–Œ≥°µÿµƒ√ʪ˝Œ™750m2£ø
£®2£©ƒ‹∑Ò πÀ˘Œßæÿ–Œ≥°µÿµƒ√ʪ˝Œ™810m2£¨Œ™ ≤√¥£ø
£®3£©‘ı—˘Œß≤≈ƒ‹ πŒß≥ˆµƒæÿ–Œ≥°µÿ√ʪ˝◊Ó¥Û£ø◊Ó¥Û√ʪ˝Œ™∂‡…Ÿ£ø«ÎÕ®π˝º∆À„Àµ√˜£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒfi÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com