
如图,在平面直角坐标系中,△ABC的边AB在x轴上,∠ABC=90°,AB=BC,OA=1,OB=4,抛物
线 经过A、C两点.
经过A、C两点.
(1)求抛物线的解析式及其顶点坐标;
(2)如图①,点P是抛物线上位于x轴下方的一点,点Q与点P关于抛物线的对称轴对称,过点P、Q分别向x轴作垂线,垂足为点D、E,记矩形DPQE的周长为d,求d的最大值,并求出使d最大值时点P的坐标;
(3)如图②,点M是抛物线上位于直线AC下方的一点,过点M作MF⊥AC于点F,连接MC,作MN∥BC交直线AC于点N,若MN将△MFC的面积分成2:3两部分,请确定M点的坐标.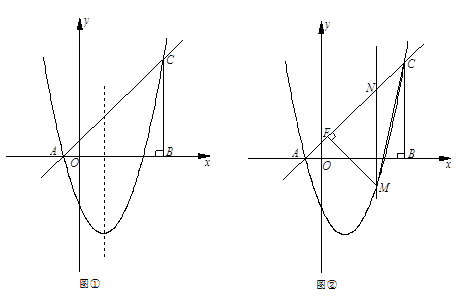
(1)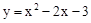 ,(1,
,(1,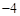 );(2)(0,
);(2)(0,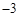 )或(2,
)或(2,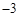 );(3)
);(3)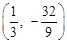 或
或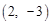 .
.
解析试题分析:(1)根据曲线上点的坐标与方程的关系,将A(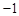 ,0)C(4,5)代入
,0)C(4,5)代入 得方程组,解之即可得抛物线的解析式;化为顶点式即可得顶点坐标.
得方程组,解之即可得抛物线的解析式;化为顶点式即可得顶点坐标.
(2)点P为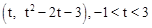 ,分
,分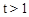 和
和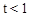 ,把矩形DPQE的周长表示为
,把矩形DPQE的周长表示为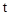 的二次函数,应用二次函数最值原理求解即可.
的二次函数,应用二次函数最值原理求解即可.
(3)分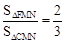 和
和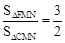 两种情况讨论即可.
两种情况讨论即可.
(1)由已知得:A(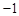 ,0)、C(4,5),
,0)、C(4,5),
∵二次函数 的图像经过点A(-1,0)C(4,5),
的图像经过点A(-1,0)C(4,5),
∴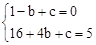 , 解得
, 解得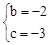 .
.
∴抛物线解析式为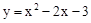 .
.
∵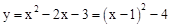 ,∴顶点坐标为(1,
,∴顶点坐标为(1,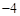 ).
).
(2)如答图①,由(1)知抛物线的对称轴为直线x=1,
设点P为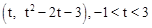 ,
,
∵P、Q为抛物线上的对称点,∴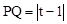 .
.
当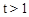 时,
时,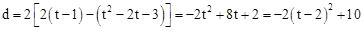 ,
,
∵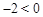 ,∴当t=2使,d有最大值为10,即点P为(2,
,∴当t=2使,d有最大值为10,即点P为(2,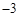 )
)
当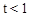 时,由抛物线的轴对称性得,点P为(0,
时,由抛物线的轴对称性得,点P为(0,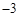 )时,d有最大值10
)时,d有最大值10
综上所述,当P为(0,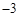 )或(2,
)或(2,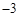 )时,d有最大值10
)时,d有最大值10
(3)如答图②,过点F作FH⊥MN于H,过C作CG⊥MN于G,则∠ANM=∠ACB=45°.
∵MF⊥AC,∴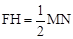 . ∴
. ∴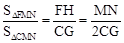 .
.
∵A(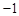 ,0),C(4,5),∴直线AC解析式为y=x+1.
,0),C(4,5),∴直线AC解析式为y=x+1.
设点M为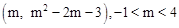 ,则CG=4-m.
,则CG=4-m.
由MN∥BC得点N为(m,m+1),
∴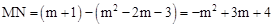 .
.
当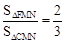 时,有3MN="4CG" ,即
时,有3MN="4CG" ,即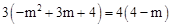 ,
,
解得: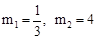 (舍去).
(舍去).
∴点M为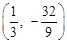 .
.
当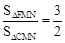 时,有MN=3CG, 即
时,有MN=3CG, 即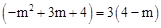 ,
,
解得: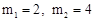 (舍去).
(舍去).
∴点M为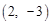 .
.
综上所述,当M为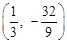 或
或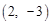 时,MN将△MFC的面积分成2:3两部分.
时,MN将△MFC的面积分成2:3两部分. 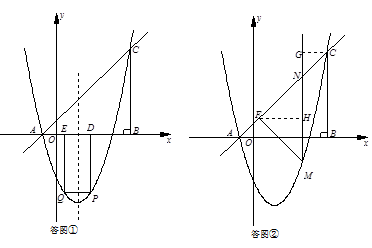
考点:1.二次函数综合题;2.曲线上点的坐标与方程的关系;3.二次函数的性质;4.解一元二次方程;5.分类思想的应用.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:解答题
如图1,抛物线 与
与 轴交于
轴交于 两点,与
两点,与 轴交于点
轴交于点 ,连结AC,若
,连结AC,若
(1)求抛物线的解析式;
(2)抛物线对称轴上有一动点P,当 时,求出点
时,求出点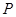 的坐标;
的坐标;
(3)如图2所示,连结 ,
, 是线段
是线段 上(不与
上(不与 、
、 重合)的一个动点.过点
重合)的一个动点.过点 作直线
作直线 ,交抛物线于点
,交抛物线于点 ,连结
,连结 、
、 ,设点
,设点 的横坐标为.当t为何值时,
的横坐标为.当t为何值时, 的面积最大?最大面积为多少?
的面积最大?最大面积为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图①,在□ABCD中,对角线AC⊥AB,BC=10,tan∠B=2.点E是BC边上的动点,过点E作EF⊥BC于点E,交折线AB-AD于点F,以EF为边在其右侧作正方形EFGH,使EH边落在射线BC上.点E从点B出发,以每秒1个单位的速度在BC边上运动,当点E与点C重合时,点E停止运动,设点E的运动时间为t( )秒.
)秒.
(1)□ABCD的面积为 ;当t= 秒时,点F与点A重合;
(2)点E在运动过程中,连接正方形EFGH的对角线EG,得△EHG,设△EHG与△ABC的重叠部分面积为S,请直接写出S与t的函数关系式以及对应的自变量t的取值范围;
(3)作点B关于点A的对称点Bˊ,连接CBˊ交AD边于点M(如图②),当点F在AD边上时,EF与对角线AC交于点N,连接MN得△MNC.是否存在时间t,使△MNC为等腰三角形?若存在,请求出使△MNC为等腰三角形的时间t;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在直角坐标平面内,O为原点,抛物线 经过点A(6,0),且顶点B(m,6)在直线
经过点A(6,0),且顶点B(m,6)在直线 上.
上.
(1)求m的值和抛物线 的解析式;
的解析式;
(2)如在线段OB上有一点C,满足 ,在x轴上有一点D(10,0),连接DC,且直线DC与y轴交于点E.
,在x轴上有一点D(10,0),连接DC,且直线DC与y轴交于点E.
①求直线DC的解析式;
②如点M是直线DC上的一个动点,在x轴上方的平面内有另一点N,且以O、E、M、N为顶点的四边形是菱形,请直接写出点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图1,把边长分别是为4和2的两个正方形纸片OABC和OD′E′F′叠放在一起.
(1)操作1:固定正方形OABC,将正方形OD′E′F′绕点O按顺时针方向旋转45°得到正方形ODEF,如图2,连接AD、CF,线段AD与CF之间有怎样的数量关系?试证明你的结论;
(2)操作2,如图2,将正方形ODEF沿着射线DB以每秒1个单位的速度平移,平移后的正方形ODEF设为正方形PQMN,如图3,设正方形PQMN移动的时间为x秒,正方形PQMN与正方形OABC的重叠部分面积为y,直接写出y与x之间的函数解析式;
(3)操作3:固定正方形OABC,将正方形OD′E′F′绕点O按顺时针方向旋转90°得到正方形OHKL,如图4,求△ACK的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图(1),直线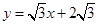 与x轴交于点A、与y轴交于点D,以AD为腰,以x轴为底作等腰梯形ABCD(AB>CD),且等腰梯形的面积是8
与x轴交于点A、与y轴交于点D,以AD为腰,以x轴为底作等腰梯形ABCD(AB>CD),且等腰梯形的面积是8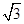 ,抛物线经过等腰梯形的四个顶点.
,抛物线经过等腰梯形的四个顶点.
图(1)
(1) 求抛物线的解析式;
(2) 如图(2)若点P为BC上的—个动点(与B、C不重合),以P为圆心,BP长为半径作圆,与 轴的另一个交点为E,作EF⊥AD,垂足为F,请判断EF与⊙P的位置关系,并给以证明;
轴的另一个交点为E,作EF⊥AD,垂足为F,请判断EF与⊙P的位置关系,并给以证明;
图(2)
(3) 在(2)的条件下,是否存在点P,使⊙P与y轴相切,如果存在,请求出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,某种新型导弹从地面发射点L处发射,在初始竖直加速飞行阶段,导弹上升的高度y(km)与飞行时间x(s)之间的关系式为y= x2+
x2+ x(0≤x≤10).发射3 s后,导弹到达A点,此时位于与L同一水面的R处雷达站测得AR的距离是2 km,再过3 s后,导弹到达B点.
x(0≤x≤10).发射3 s后,导弹到达A点,此时位于与L同一水面的R处雷达站测得AR的距离是2 km,再过3 s后,导弹到达B点.
(1)求发射点L与雷达站R之间的距离;
(2)当导弹到达B点时,求雷达站测得的仰角(即∠BRL)的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,直角坐标系中Rt△ABO,其顶点为A(0, 1)、B(2, 0)、O(0, 0),将此三角板绕原点O逆时针旋转90°,得到Rt△A′B′O.
(1)一抛物线经过点A′、B′、B,求该抛物线的解析式;
(2)设点P是在第一象限内抛物线上的一动点,是否存在点P,使四边形PB′A′B的面积是△A′B′O面积4倍?若存在,请求出P的坐标;若不存在,请说明理由.
(3)在(2)的条件下,试指出四边形PB′A′B是哪种形状的四边形?并写出四边形PB′A′B的两条性质.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com