
如图,在直角坐标平面内,O为原点,抛物线 经过点A(6,0),且顶点B(m,6)在直线
经过点A(6,0),且顶点B(m,6)在直线 上.
上.
(1)求m的值和抛物线 的解析式;
的解析式;
(2)如在线段OB上有一点C,满足 ,在x轴上有一点D(10,0),连接DC,且直线DC与y轴交于点E.
,在x轴上有一点D(10,0),连接DC,且直线DC与y轴交于点E.
①求直线DC的解析式;
②如点M是直线DC上的一个动点,在x轴上方的平面内有另一点N,且以O、E、M、N为顶点的四边形是菱形,请直接写出点N的坐标.
(1)3, ;(2)①
;(2)① ;②(-5,
;②(-5, )或(4,8)或
)或(4,8)或 .
.
解析试题分析:(1)先根据抛物线 的顶点B(m,6)在直线
的顶点B(m,6)在直线 上可求出m的值,再用待定系数发即可求出此抛物线的解析式.
上可求出m的值,再用待定系数发即可求出此抛物线的解析式.
(2)①作CH⊥OA,BG⊥OA,再根据平行线分线段成比例定理即可得出CH的长,进而求出C点坐标,再根据D点坐标用待定系数法即可求出直线DC解析式.
②根据菱形的性质即可求出符合条件的N点坐标.
(1)∵顶点B(m,6)在直线 上,∴m="3." ∴B(3,6).
上,∴m="3." ∴B(3,6).
把A、B两点坐标代入抛物线的解析式得, ,解得
,解得 .
.
∴抛物线的解析式为: .
.
(2)①如图1,作CH⊥OA,BG⊥OA,
∴CH∥BG,∴△OCH∽△OBG. ∴ .
.
∵OC=2CB,∴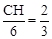 ,即CH="4." ∴点C的坐标为(2,4).
,即CH="4." ∴点C的坐标为(2,4).
∵D(10,0),∴根据题意 ,解得:
,解得: .
.
∴直线DC解析式 .
.
②如图2:∵四边形ENOM是菱形,∴OS=ES= OE=
OE= . ∴NK=
. ∴NK= .
.
∵ON∥DE,∴tan∠NOK=tan∠EDO= .∴OK=5.∴N1(-5,
.∴OK=5.∴N1(-5, ).
).
如图3:∵EM⊥OB,∴ON=2OC.
∵点C的坐标为(2,4),∴N2(4,8).
③如图4:∵直线DC解析式 ,∴E(0,5).
,∴E(0,5).
设M(x, ),
),
∵四边形ENOM是菱形,∴EM=OE=5,即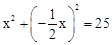 ,解得x=
,解得x= .∴M
.∴M .
.
∴可设N( ,y),则
,y),则 ,解得y=
,解得y= 或y=
或y=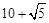 (舍去).∴N3
(舍去).∴N3 .
.
综上所述,点N的坐标为(-5, )或(4,8)或
)或(4,8)或 .
.
考点:1.二次函数综合题;2.动点问题;3.曲线上点的坐标与方程的关系;4.相似三角形的判定和性质;5.锐角三角函数定义;6.菱形的性质;7.分类思想的应用.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:解答题
在平面直角坐标系中,已知抛物线 (b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,–1),C的坐标为(4,3),直角顶点B在第四象限.
(b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,–1),C的坐标为(4,3),直角顶点B在第四象限.
(1)如图,若该抛物线过A,B两点,求b,c的值;
(2)平移(1)中的抛物线,使顶点P在直线AC上滑动,且与直线AC交于另一点Q.
①点M在直线AC下方,且为平移前(1)中的抛物线上的点,当以M,P,Q三点为顶点的三角形是以PQ为腰的等腰直角三角形时,求点M的坐标;
②取BC的中点N,连接NP,BQ.当 取最大值时,点Q的坐标为________.
取最大值时,点Q的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图1,抛物线y=-x2+bx+c的顶点为Q,与x轴交于A(-1,0)、B(5,0)两点,与y轴交于点C.
(1)求抛物线的解析式及其顶点Q的坐标;
(2)在该抛物线的对称轴上求一点P,使得△PAC的周长最小,请在图中画出点P的位置,并求点P的坐标;
(3)如图2,若点D是第一象限抛物线上的一个动点,过D作DE⊥x轴,垂足为E.
①有一个同学说:“在第一象限抛物线上的所有点中,抛物线的顶点Q与x轴相距最远,所以当点D运动至点Q时,折线D-E-O的长度最长”,这个同学的说法正确吗?请说明理由.
②若DE与直线BC交于点F.试探究:四边形DCEB能否为平行四边形?若能,请直接写出点D的坐标;若不能,请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在平面直角坐标系 中,抛物线
中,抛物线 与x轴交于点A(-2,0)和点B,与y轴交于点C(0,
与x轴交于点A(-2,0)和点B,与y轴交于点C(0, ),线段AC上有一动点P从点A出发,以每秒1个单位长度的速度向点C移动,线段AB上有另一个动点Q从点B出发,以每秒2个单位长度的速度向点A移动,两动点同时出发,设运动时间为t秒.
),线段AC上有一动点P从点A出发,以每秒1个单位长度的速度向点C移动,线段AB上有另一个动点Q从点B出发,以每秒2个单位长度的速度向点A移动,两动点同时出发,设运动时间为t秒.
(1)求该抛物线的解析式;
(2)在整个运动过程中,是否存在某一时刻,使得以A,P,Q为顶点的三角形与△AOC相似?如果存在,请求出对应的t的值;如果不存在,请说明理由.
(3)在y轴上有两点M(0,m)和N(0,m+1),若要使得AM+MN+NP的和最小,请直接写出相应的m、t的值以及AM+MN+NP的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,△ABC的边AB在x轴上,∠ABC=90°,AB=BC,OA=1,OB=4,抛物线 经过A、C两点.
经过A、C两点.
(1)求抛物线的解析式及其顶点坐标;
(2)如图①,点P是抛物线上位于x轴下方的一点,点Q与点P关于抛物线的对称轴对称,过点P、Q分别向x轴作垂线,垂足为点D、E,记矩形DPQE的周长为d,求d的最大值,并求出使d最大值时点P的坐标;
(3)如图②,点M是抛物线上位于直线AC下方的一点,过点M作MF⊥AC于点F,连接MC,作MN∥BC交直线AC于点N,若MN将△MFC的面积分成2:3两部分,请确定M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,△ABC的边AB在x轴上,∠ABC=90°,AB=BC,OA=1,OB=4,抛物
线 经过A、C两点.
经过A、C两点.
(1)求抛物线的解析式及其顶点坐标;
(2)如图①,点P是抛物线上位于x轴下方的一点,点Q与点P关于抛物线的对称轴对称,过点P、Q分别向x轴作垂线,垂足为点D、E,记矩形DPQE的周长为d,求d的最大值,并求出使d最大值时点P的坐标;
(3)如图②,点M是抛物线上位于直线AC下方的一点,过点M作MF⊥AC于点F,连接MC,作MN∥BC交直线AC于点N,若MN将△MFC的面积分成2:3两部分,请确定M点的坐标.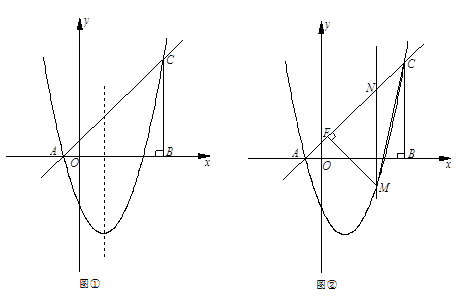
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某经销商代理销售一种手机,按协议,每卖出一部手机需另交品牌代理费100元,已知该种手机每部进价800元,销售单价为1200元时,每月能卖出100部,市场调查发现,若每部手机每让利50元,则每月可多售出40部.
(1)若每月要获取36000元利润,求让利价
(利润=销售收入-进货成本-品牌代理费)
(2)设让利x元,月利润为y元,写出y与x的函数关系式,并求让利多少元时,月利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知直线y=x与抛物线y= x2交于A、B两点.
x2交于A、B两点.
(1)求交点A、B的坐标;
(2)记一次函数y=x的函数值为y1,二次函数y= x2的函数值为y2.若y1>y2,求x的取值范围.
x2的函数值为y2.若y1>y2,求x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com