
【题目】如图,Rt△ABC中,∠BAC=90°,AB=2,AC=4,D是BC边上一动点,G是BC边上的一动点,GE∥AD分别交AC、BA或其延长线于F、E两点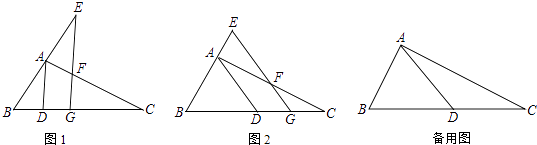
(1)如图1,当BC=5BD时,求证:EG⊥BC;
(2)如图2,当BD=CD时,FG+EG是否发生变化?证明你的结论;
(3)当BD=CD,FG=2EF时,DG的值= .
【答案】
(1)
证明:如图1,

∵∠BAC=90°,AB=2,AC=4,
∴BC=2 ![]() ,
,
∵BC=5BD,
∴BD= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]()
又∵∠DBA=∠ABC,
∴△BDA∽△BAC,
∴∠BDA=∠BAC=90°,
∵EG∥AD,
∴EG⊥BC.
(2)
证明:FG=EG=2 ![]() 不变,
不变,
证法1:如图2,

∵EG∥AD,
∴△CFG∽△CAD,
∴ ![]() =
= ![]() ,
,
同理 ![]() =
= ![]() ,
,
∵BD=CD,
∴ ![]() +
+ ![]() =
= ![]() +
+ ![]() =2,
=2,
∴EG+FG=2AD,
∵BD=CD,∠BAC=90°,
∴AD= ![]() BC=
BC= ![]() ,
,
∴EG+FG=2AD=2 ![]() .
.
证法2:如图3,
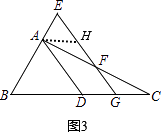
取EF的中点,易证四边形ADGH是平行四边形,
得出EG+FG=2GH=2AD=2 ![]() .
.
证法3:如图4,

中线AD加倍到M,易证四边形AMNE是平行四边形,
得出EG+FG=EN=AM=2AD=2 ![]() .
.
(3)![]()
或 ![]()
【解析】(3)如图5,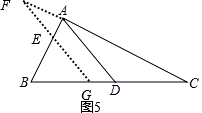
当BD=CD,FG=2EF时,
则GE=EF,
∵GE∥AD,AD∥GF,
∴△CFG∽△CAD,△ABD∽△BGE,
∴ ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ;
;
又BG+CG=2 ![]() ,
,
∴BG= ![]()
![]() ,
,
∴DG=BD=BG= ![]() ;
;
如图6,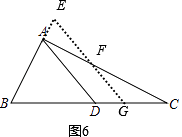
当BD=CD,FG=2EF时,
则GE=EF,
∵GE∥AD,AD∥GF,
∴△CFG∽△CAD,△ABD∽△AGE,
∴ ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ;
;
又BG+CG=2 ![]() ,
,
∴CG= ![]()
![]() ,
,
∴DG=CD﹣CG= ![]() .
.
综上所知DG为 ![]() 或
或 ![]() .
.
【考点精析】利用勾股定理的概念对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上. 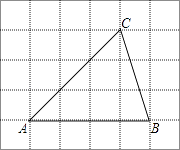
(1)△ABC的面积等于;
(2)若四边形DEFG是△ABC中所能包含的面积最大的正方形,请你在如图所示的网格中,用直尺和三角尺画出该正方形,并简要说明画图方法(不要求证明) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人从A城出发,前往距离A城30千米的B城.现在有三种方案供他选择:
①骑自行车,其速度为15千米/时;
②蹬三轮车,其速度为10千米/时;
③骑摩托车,其速度为40千米/时.
(1)选择哪种方式能使他从A城到达B城的时间不超过2小时?请说明理由;
(2)设此人在行进途中离B城的距离为s(千米),行进时间为t(时),就(1)所选定的方案,试写出s与t之间的函数关系式(注明自变量t的取值范围),并在如图所示的平面直角坐标系中画出函数的图象.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件20元,售价为每件25元时,每天可卖出250件.市场调查反映:如果调整价格,一件商品每涨价1元,每天要少卖出10件.
(1)求出每天所得的销售利润w(元)与每件涨价x(元)之间的函数关系式;
(2)求销售单价为多少元时,该商品每天的销售利润最大;
(3)商场的营销部在调控价格方面,提出了A,B两种营销方案.
方案A:每件商品涨价不超过5元;
方案B:每件商品的利润至少为16元.
请比较哪种方案的最大利润更高,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网络中,△ABC的三个顶点都在格点上,点A、B、C的坐标分别为(﹣2,4)、(﹣2,0)、(﹣4,1),将△ABC绕原点O旋转180度得到△A1B1C1 . 结合所给的平面直角坐标系解答下列问题: 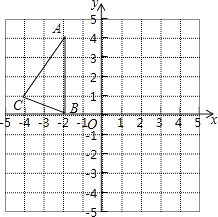
(1)画出△A1B1C1;
(2)画出一个△A2B2C2 , 使它分别与△ABC,△A1B1C1轴对轴(其中点A,B,C与点A2 , B2 , C2对应);
(3)在(2)的条件下,若过点B的直线平分四边形ACC2A2的面积,请直接写出该直线的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=x2+bx﹣5的图象的对称轴是经过点(2,0)且平行于y轴的直线,则关于x的方程x2+bx=5的解为( )
A.x1=0,x2=4
B.x1=1,x2=5
C.x1=1,x2=﹣5
D.x1=﹣1,x2=5
查看答案和解析>>
科目:初中数学 来源: 题型:
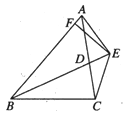
【题目】如图BD为△ABC的角平分线,且BD=BC, E为BD延长线上一点,BE=BA,
过E作EF⊥AB于F,下列结论:
①△ABD≌△EBC ;②∠BCE+∠BDC=180°;
③AD=AE=EC;④AB//CE ;
⑤BA+BC=2BF.其中正确的是________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E. 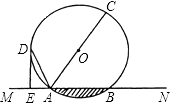
(1)求证:DE是⊙O的切线;
(2)若DE=6,AE= ![]() ,求⊙O的半径;
,求⊙O的半径;
(3)在第(2)小题的条件下,则图中阴影部分的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(a,b),B(c,0),|a-3|+(2b-c)2+![]() =0.
=0.

(1)求点A,B的坐标;
(2)如图,点C为x轴正半轴上一点,且OC=OA,点D为OC的中点,连AC,AD,请探索AD+CD与![]() AC之间的大小关系,并说明理由;
AC之间的大小关系,并说明理由;

(3)如图,过点A作AE⊥y轴于E,F为x轴负半轴上一动点( 不与(-3,0)重合 ),G在EF延长线上,以EG为一边作∠GEN=45°,过A作AM⊥x轴,交EN于点M,连FM,当点F在x轴负半轴上移动时,式子![]() 的值是否发生变化?若变化,求出变化的范围;若不变化,请求出其值并说明理由.
的值是否发生变化?若变化,求出变化的范围;若不变化,请求出其值并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com