
 甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示,根据图象信息解答下列问题:
甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示,根据图象信息解答下列问题:分析 (1)直接由图象可知.
(2)求出甲乙两个函数的解析式,解方程组即可.
(3)转化为两个方程:60x-(100x-100)=50或100x-100-60x=50解决.
解答 解:(1)由图象可知乙车比甲车晚出发1个小时.
(2)设甲的函数解析式为y=kx,把点(5,300)代入得到k=60,故y=60x,
设乙的函数解析式为y=k′x+b,把点(1,0)和点(4,300)代入得到$\left\{\begin{array}{l}{k′+b=0}\\{4k′+b=300}\end{array}\right.$解得$\left\{\begin{array}{l}{k′=100}\\{b=-100}\end{array}\right.$故y=100x-100,
由$\left\{\begin{array}{l}{y=60x}\\{y=100x-100}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{5}{2}}\\{y=150}\end{array}\right.$,
$\frac{5}{2}-1$=$\frac{3}{2}$=1.5
所以乙车出发后1.5小时追上甲车.
(3)由题意:60x-(100x-100)=50或100x-100-60x=50
解得到x=$\frac{5}{4}$或$\frac{15}{4}$,
因为$\frac{5}{4}$-1=$\frac{1}{4}$,$\frac{15}{4}$-1=$\frac{11}{4}$,
所以求乙车出发$\frac{1}{4}$或$\frac{11}{4}$小时,两车相距50千米.
点评 本题考查用待定系数法一次函数的解析式、相遇问题转化为求方程组交点坐标,学会用方程的思想解决实际问题.


科目:初中数学 来源: 题型:选择题
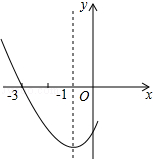 如图,开口向上的抛物线y=ax2+bx+c的对称轴为直线x=-1,且过点(-3,0),下列说法:①abc<0;②b-2a=0;③4a+2b+c<0;④若($\frac{5}{2}$,y1),(-5,y2)是抛物线上两点,则y1<y2.其中正确的个数是( )
如图,开口向上的抛物线y=ax2+bx+c的对称轴为直线x=-1,且过点(-3,0),下列说法:①abc<0;②b-2a=0;③4a+2b+c<0;④若($\frac{5}{2}$,y1),(-5,y2)是抛物线上两点,则y1<y2.其中正确的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com