
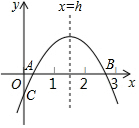
 二次函数y=ax2+bx+c(a≠0)的大致图象如图所示(1<x=h<2,0<xA<1).下列结论:①2a+b>0;②abc<0; ③若OC=2OA,则2b-ac=4; ④3a-c<0.其中正确的个数是( )
二次函数y=ax2+bx+c(a≠0)的大致图象如图所示(1<x=h<2,0<xA<1).下列结论:①2a+b>0;②abc<0; ③若OC=2OA,则2b-ac=4; ④3a-c<0.其中正确的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①根据抛物线的开口向下即可得出a<0,再根据抛物线的对称轴在x=1和x=2之间即可得出b>-2a,①正确;②由b>-2a可得出b>0,再根据抛物线与y轴交于y轴负半轴可得出c<0,由此即可得出abc>0,②错误;③根据求根公式表示出点A的横坐标,结合OC=2OA即可得出2b-ac=4,③正确;④根据抛物线的对称轴1<-$\frac{b}{2a}$<2可得出-2a<b<-4a,再由当x=1时y>0即可得出a+b+c>0,进而即可得出3a-c<0,④正确.综上即可得出结论.
解答 解:①∵抛物线的开口向下,
∴a<0.
∵抛物线的对称轴-$\frac{b}{2a}$>1,
∴b>-2a,即2a+b>0,①成立;
②∵b>-2a,a<0,
∴b>0,
∵抛物线与y轴的交点在y轴的负半轴,
∴c<0,
∴abc>0,②错误;
③点A的横坐标为$\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$,点C的纵坐标为c,
∵OC=2OA,
∴-c=$\frac{-b-\sqrt{{b}^{2}-4ac}}{a}$,整理得:2b-ac=4,③成立;
④∵抛物线的对称轴1<-$\frac{b}{2a}$<2,
∴-2a<b<-4a,
∵当x=1时,y=a+b+c>0,
∴a-4a+c>0,即3a-c<0,④正确.
综上可知正确的结论有3个.
故选C.
点评 本题考查了二次函数图象与系数的关系,根据二次函数的图象找出系数间的关系是解题的关键.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:解答题
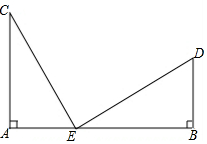 如图,已知AC⊥AB,DB⊥AB,AC=BE,CE=DE,
如图,已知AC⊥AB,DB⊥AB,AC=BE,CE=DE,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
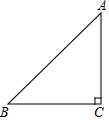 在△ABC中,AC=BC,∠ACB=90°,CE是过C点的一条直线,AD⊥CE于D,BE⊥CE于E,DE=4cm,AD=2cm,则BE=( )
在△ABC中,AC=BC,∠ACB=90°,CE是过C点的一条直线,AD⊥CE于D,BE⊥CE于E,DE=4cm,AD=2cm,则BE=( )| A. | 2cm | B. | 4cm | C. | 6cm或2cm | D. | 6cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (1+20%m)万元 | B. | (m+20%)万元 | C. | $\frac{6}{5}$m万元 | D. | 20% m 万元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
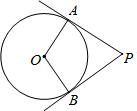 如图,PA、PB是⊙O的切线,切点是A、B,已知∠P=60°,OA=3,那么劣弧$\widehat{AB}$的长度为( )
如图,PA、PB是⊙O的切线,切点是A、B,已知∠P=60°,OA=3,那么劣弧$\widehat{AB}$的长度为( )| A. | 6π | B. | 5π | C. | 3π | D. | 2π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com