解:(1)证明:∵四边形ABCD是矩形,
∴∠ECD=∠ADE=∠AOD=90°,
∴∠ADO+∠EDC=90°,∠OAD+∠ADO=90°,
∴∠OAD=∠EDC
∴△AOD∽△DCE;
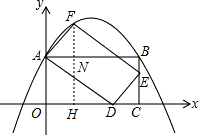
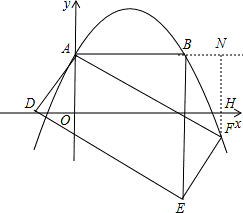
(2)解:①过F作FH⊥OC角OC于H,交AB于N,
由题意得,AB=OC=7,AO=BC=4,OD=5,CD=2
∵△AOD∽△DCE,
∴
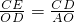
,即:
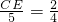
,
∴CE=

,
∵四边形ADEF是矩形,DE=AF,∠DAB+∠BAF=90°
又∵∠OAD+∠DAB=90°
∴∠OAD=∠BAF,
∴△AFN≌△DEC
∴AN=DC=2,FN=EC=

,
∴FH=

,
∴F点的坐标为(2,

),
由A(0.4),设A、F、B三点的抛物线的解析式为y=ax
2+bx+4
由F(2,

)、B(7,4),
得
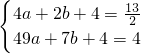
,解得:
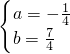
∴过A、F、B三点的解析式为:y=-

x
2+

x+4,
②理由是:由(2)中①可知,抛物线的解析式为:y=-

x
2+

x+4,
当D(k,0)时,则OD=k,DC=7-k,
同理,由△AOD∽△DCE和△AFN≌△DEC求得:FN=CE=
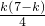
,AN=7-K,
∴F(7-k,4+
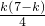
),
将x=7-k代入y=-

x
2+

x+4,
得y=
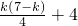
,
∴点F仍在①中所求的抛物线上.
(3)如图,点F还在①中所求的抛物线上,
理由是:过点F作直线FH⊥OC交OC于点H,交直线AB于N,
由(2)中①可知,抛物线的表达式为y=-

x
2+

x+4,
点D(k,0),k<0时,则OD=-k,DC=7-k,
同理,由△AOD∽△DCE和△AFN≌△DEC求得:FN=CE=
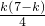
,AN=DC=7-K,
当FN≥4时,点F在x轴的上方,
FH=FN-4=-
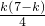
-4,点F的纵坐标是
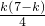
+4,
当FN<4时,点F在x轴的上方
FH=4-FN=4+
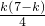
,点F的纵坐标也是
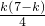
+4,
故F(7-k,4+
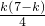
)
由(2)②可知点F在①中所求的抛物线上.
分析:(1)利用矩形的性质得到∠OAD=∠EDC后利用两角对应相等的两三角形相似证明即可;
(2)过F作FH⊥OC角OC于H,交AB于N,利用△AOD∽△DCE得到比例式求得CE的长,从而求得AFN≌△DEC,利用全等三角形的性质得到F点的坐标后利用待定系数法求得函数的解析式即可得到结论;
(3)利用以上两个小题中证得的全等和相似分当FN≥4时,点F在x轴的上方和当FN<4时,点F在x轴的上方两种情况求得点F的坐标即可.
点评:本题是二次函数的综合题型,其中涉及到的几何知识与函数知识的结合的题目更是近几年中考的热点考题之一.在求有关存在性问题时要注意分析题意分情况讨论结果.



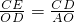 ,即:
,即: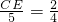 ,
, ,
, ,
, ,
, ),
), )、B(7,4),
)、B(7,4),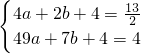 ,解得:
,解得: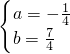
 x2+
x2+ x+4,
x+4, x2+
x2+ x+4,
x+4,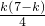 ,AN=7-K,
,AN=7-K,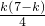 ),
), x2+
x2+ x+4,
x+4,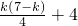 ,
, x2+
x2+ x+4,
x+4,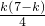 ,AN=DC=7-K,
,AN=DC=7-K,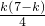 -4,点F的纵坐标是
-4,点F的纵坐标是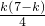 +4,
+4,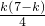 ,点F的纵坐标也是
,点F的纵坐标也是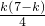 +4,
+4,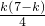 )
)


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案 =2
=2
 如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.
如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.