
ФГЩЬГЁЪдЯњвЛжжГЩБОЮЊУПМў60дЊЕФЗўзАЃЌЙцЖЈЪдЯњЦкМфЯњЪлЕЅМлВЛЕЭгкГЩБОЕЅМлЃЌЧвЛёРћВЛЕУИпгк50%ЃЎОЪдЯњЗЂЯжЃЌЯњЪлСПPЃЈМўЃЉгыЯњЪлЕЅМлxЃЈдЊЃЉЗћКЯвЛДЮКЏЪ§ЙиЯЕЃЌЕБЯњЪлЕЅМлЮЊ65дЊЪБЯњЪлСПЮЊ55МўЃЌЕБЯњЪлЕЅМлЮЊ75дЊЪБЯњЪлСПЮЊ45МўЃЎ
ЃЈЂёЃЉЧѓPгыxЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈЂђЃЉШєИУЩЬГЁЛёЕУРћШѓЮЊyдЊЃЌЪдаДГіРћШѓyгыЯњЪлЕЅМлxжЎМфЕФЙиЯЕЪНЃЛ
ЃЈЂѓЃЉЯњЪлЕЅМлЖЈЮЊЖрЩйдЊЪБЃЌЩЬГЁПЩЛёЕУзюДѓРћШѓЃЌзюДѓРћШѓЪЧЖрЩйдЊЃП

| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКЧрКЃЪЁ2018ФъжаПМФЃФтЪдОэЃЈ4дТЗнЃЉЪ§бЇЪдОэ ЬтаЭЃКЕЅбЁЬт
ЯТСаЫФеХгЁгаЦћГЕЦЗХЦБъжОЭМАИЕФПЈЦЌжаЃЌЪЧжааФЖдГЦЭМаЮЕФПЈЦЌЪЧЃЈЁЁЁЁЃЉ
A.  B.
B.  C.
C.  D.
D. 
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКеуНЪЁсщжнЪа2018-2019бЇФъЦпФъМЖЩЯбЇЦкЦкжаПМЪдЪ§бЇЪдОэ ЬтаЭЃКНтД№Ьт
ЃЈ1ЃЉВФСЯ1ЃКвЛАуЕиЃЌnИіЯрЭЌвђЪ§aЯрГЫЃК МЧЮЊ
МЧЮЊ  Шч
Шч ЃЌДЫЪБЃЌ3Назівд2ЮЊЕзЕФ8ЕФЖдЪ§ЃЌМЧЮЊlog28ЃЈМДlog28=3ЃЉЃЎФЧУДЃЌlog39=________ЃЌ
ЃЌДЫЪБЃЌ3Назівд2ЮЊЕзЕФ8ЕФЖдЪ§ЃЌМЧЮЊlog28ЃЈМДlog28=3ЃЉЃЎФЧУДЃЌlog39=________ЃЌ =________ЃЛ
=________ЃЛ
ЃЈ2ЃЉВФСЯ2ЃКаТЙцЖЈвЛжждЫЫуЗЈдђЃКздШЛЪ§1ЕНnЕФСЌГЫЛ§гУnЃЁБэЪОЃЌР§ШчЃК1ЃЁ=1ЃЌ2ЃЁ=2ЁС1=2ЃЌ3ЃЁ=3ЁС2ЁС1=6ЃЌ4ЃЁ=4ЁС3ЁС2ЁС1=24ЃЌЁдкетжжЙцЖЈЯТЃЌЧыФуНтОіЯТСаЮЪЬтЃК
ЂйЫу5ЃЁ=________ЃЛ
ЂквбжЊxЮЊећЪ§ЃЌЧѓГіТњзуИУЕШЪНЕФ .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКеуНЪЁсщжнЪа2018-2019бЇФъЦпФъМЖЩЯбЇЦкЦкжаПМЪдЪ§бЇЪдОэ ЬтаЭЃКЕЅбЁЬт
Шє


A. 
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКББОЉЪІДѓИНжа2018НьОХФъМЖЃЈЯТЃЉЦкжаЪ§бЇФЃФтЪдОэ ЬтаЭЃКНтД№Ьт
ЯШдФЖСЯТУцвЛЖЮВФСЯЃЌдйЭъГЩКѓУцЕФЮЪЬтЃК
ВФСЯЃКЙ§ХзЮяЯпy=ax2ЃЈaЃО0ЃЉЕФЖдГЦжсЩЯвЛЕуЃЈ0ЃЌЉ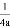 ЃЉзїЖдГЦжсЕФДЙЯпlЃЌдђХзЮяЯпЩЯШЮвтвЛЕуPЕНЕуFЃЈ0ЃЌ
ЃЉзїЖдГЦжсЕФДЙЯпlЃЌдђХзЮяЯпЩЯШЮвтвЛЕуPЕНЕуFЃЈ0ЃЌ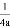 ЃЉЕФОрРыгыPЕНlЕФОрРывЛЖЈЯрЕШЃЌЮвУЧНЋЕуFгыжБЯпlЗжБ№ГЦзїетХзЮяЯпЕФНЙЕуКЭзМЯпЃЌШчy=x2ЕФНЙЕуЮЊЃЈ0ЃЌ
ЃЉЕФОрРыгыPЕНlЕФОрРывЛЖЈЯрЕШЃЌЮвУЧНЋЕуFгыжБЯпlЗжБ№ГЦзїетХзЮяЯпЕФНЙЕуКЭзМЯпЃЌШчy=x2ЕФНЙЕуЮЊЃЈ0ЃЌ ЃЉЃЎ
ЃЉЃЎ
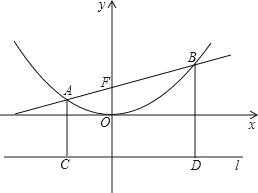
ЮЪЬтЃКШєжБЯпy=kx+bНЛХзЮяЯпy= x2гкAЁЂBЁЂACЁЂBDДЙжБгкХзЮяЯпЕФзМЯпlЃЌДЙжБзуЗжБ№ЮЊCЁЂDЃЈШчЭМЃЉЃЎ
x2гкAЁЂBЁЂACЁЂBDДЙжБгкХзЮяЯпЕФзМЯпlЃЌДЙжБзуЗжБ№ЮЊCЁЂDЃЈШчЭМЃЉЃЎ
ЂйЧѓХзЮяЯпy= x2ЕФНЙЕуFЕФзјБъЃЛ
x2ЕФНЙЕуFЕФзјБъЃЛ
ЂкЧѓжЄЃКжБЯпABЙ§НЙЕуЪБЃЌCFЁЭDFЃЛ
ЂлЕБжБЯпABЙ§ЕуЃЈЉ1ЃЌ0ЃЉЃЌЧввдЯпЖЮABЮЊжБОЖЕФдВгызМЯпlЯрЧаЪБЃЌЧѓетЬѕжБЯпЖдгІЕФКЏЪ§НтЮіЪНЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКББОЉЪІДѓИНжа2018НьОХФъМЖЃЈЯТЃЉЦкжаЪ§бЇФЃФтЪдОэ ЬтаЭЃКЬюПеЬт
ШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯп гыжБЯп
гыжБЯп ЯрНЛгкЕуBЁЂCЃЌЕуPЮЊжБЯпBCЩЯЗНЕФХзЮяЯпЩЯЕФвЛЖЏЕуЃЌ PQЁЭxжсНЛBCгкЕуQЃЌPGЁЭBCгкЕуGЃЌЕуMЮЊЯпЖЮPQЕФжаЕуЃЌдђЯпЖЮGMЕФзюДѓжЕЮЊ_________ЃЎ
ЯрНЛгкЕуBЁЂCЃЌЕуPЮЊжБЯпBCЩЯЗНЕФХзЮяЯпЩЯЕФвЛЖЏЕуЃЌ PQЁЭxжсНЛBCгкЕуQЃЌPGЁЭBCгкЕуGЃЌЕуMЮЊЯпЖЮPQЕФжаЕуЃЌдђЯпЖЮGMЕФзюДѓжЕЮЊ_________ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКББОЉЪІДѓИНжа2018НьОХФъМЖЃЈЯТЃЉЦкжаЪ§бЇФЃФтЪдОэ ЬтаЭЃКЕЅбЁЬт
вбжЊaЁй0ЃЌдкЭЌвЛжБНЧзјБъЯЕжаЃЌКЏЪ§y=axгыy=ax2ЕФЭМЯѓгаПЩФмЪЧЃЈЁЁЁЁЃЉ

A. ЂйЂк B. ЂкЂл C. ЂйЂл D. ЂкЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃККгББЪЁеХМвПкЪа2017ЁЋ2018бЇФъЕкЖўбЇЦкЦпФъМЖЪ§бЇЦкФЉПМЪд ЬтаЭЃКЬюПеЬт
МКжЊШ§НЧаЮШ§БпГЄЗжБ№ЮЊ ЃЌ
ЃЌ ЃЌ
ЃЌ ЃЌдђДЫШ§НЧаЮЕФзюДѓБпЩЯЕФИпЕШгк_____________.
ЃЌдђДЫШ§НЧаЮЕФзюДѓБпЩЯЕФИпЕШгк_____________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃКЫеПЦАцОХФъМЖЩЯВсЕкЖўеТЖдГЦЭМаЮ-дВЕЅдЊВтЪдЪ§бЇЪдОэ ЬтаЭЃКЬюПеЬт
вбжЊЃКШчЭМЃЌ







 ЃЌдђ
ЃЌдђ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com