

分析 作A′B′交AC于E,如图,AA′=x,根据正方形的性质得∠CAD=45°,AD=CD=12,再利用平移的性质得B′A′⊥AD,于是可判断△AA′E为等腰直角三角形,则A′E=AA′=x,利用平行四边形的面积公式得到
S=-x2+12x(0≤x≤12),然后根据二次函数的性质求S的最大值.
解答 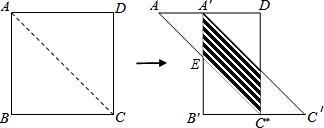 解:作A′B′交AC于E,如图,AA′=x,
解:作A′B′交AC于E,如图,AA′=x,
∵四边形ABCD为边长为12的正方形,
∴∠CAD=45°,AD=CD=12,
∵△ABC沿着AD方向平移,得到△A′B′C′,
∴B′A′⊥AD,
∴△AA′E为等腰直角三角形,
∴A′E=AA′=x,
∴S=A′E•A′D=x(12-x)=-x2+12x(0≤x≤12);
∵S=-(x-6)2+36,
∴当x=6时,S最大,最大值为36.
故答案为y=-x2+12x(0≤x≤12);6;36.
点评 本题考查了相似三角形的判定与性质,掌握平移的性质,会运用二次函数的性质解决有关最值问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 不变 | B. | 扩大为原来的5倍 | ||
| C. | 扩大为原来的10倍 | D. | 缩小为原来的$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图表示一骑自行车好一骑摩托车者沿相同路线由甲地到乙地行驶过程中行驶时间与行驶路程变化的情况.已知甲,乙两地之间的距离是60千米,请你根据此图填空,并答题:
如图表示一骑自行车好一骑摩托车者沿相同路线由甲地到乙地行驶过程中行驶时间与行驶路程变化的情况.已知甲,乙两地之间的距离是60千米,请你根据此图填空,并答题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 16 | B. | 17 | C. | 18 | D. | 19 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
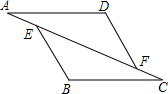 如图,已知:在△AFD和△CEB中,点A,E,F,C在同一条直线上,AE=CF,∠B=∠D,AD∥BC,请问:AD与BC相等吗?为什么?
如图,已知:在△AFD和△CEB中,点A,E,F,C在同一条直线上,AE=CF,∠B=∠D,AD∥BC,请问:AD与BC相等吗?为什么?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com