
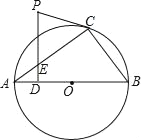
【题目】如图,△ABC内接于⊙O,AB是⊙O的直径.PC是⊙O的切线,C为切点,PD⊥AB于点D,交AC于点E.
(1)求证:∠PCE=∠PEC;
(2)若AB=10,ED=![]() ,sinA=
,sinA=![]() ,求PC的长.
,求PC的长.
【答案】(1)见解析;(2)PC=![]() .
.
【解析】
(1)由弦切角定理可知∠PCA=∠B,由直角所对的圆周角等于90°可知∠ACB=90°.由同角的余角相等可知∠AED=∠B,结合对顶角的性质可知∠PCE=∠PEC;
(2)过点P作PF⊥AC,垂足为F.由锐角三角函数的定义和勾股定理可求得AC=8,AE=![]() ,由等腰三角形三线合一的性质可知EF=
,由等腰三角形三线合一的性质可知EF=![]() ,然后证明△AED∽△PEF,由相似三角形的性质可求得PE的长,从而得到PC的长.
,然后证明△AED∽△PEF,由相似三角形的性质可求得PE的长,从而得到PC的长.
(1)∵PC是圆O的切线,
∴∠PCA=∠B.
∵AB是圆O的直径,
∴∠ACB=90°.
∴∠A+∠B=90°.
∵PD⊥AB,
∴∠A+∠AED=90°.
∴∠AED=∠B.
∵∠PEC=∠AED,
∴∠PCE=∠PEC.
(2)如图所示,过点P作PF⊥AC,垂足为F.
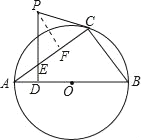
∵AB=10,sinA=![]() ,
,
∴BC=AB![]() =6.
=6.
∴AC=![]() =8.
=8.
∵DE=![]() ,sinA=
,sinA=![]() ,
,
∴AE=![]() .
.
∴EC=AC﹣AE=8﹣![]() =
=![]() .
.
∵PC=PE,PF⊥EC,
∴EF=![]() .
.
∵∠AED=∠PEF,∠EDA=∠EFP,
∴△AED∽△PEF.
∴![]() ,
,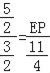 .
.
解得:EP=![]() .
.
∴PC=![]() .
.


科目:初中数学 来源: 题型:
【题目】将x1=![]() 代入反比例函数y=﹣
代入反比例函数y=﹣![]() 中,所得的函数值记为y1,将x2=y1+1代入反比例函数y=﹣
中,所得的函数值记为y1,将x2=y1+1代入反比例函数y=﹣![]() 中,所得的函数值记为y2,再将x3=y2+1代入函数y=﹣
中,所得的函数值记为y2,再将x3=y2+1代入函数y=﹣![]() 中,所得的函数值记为y3…,将xn=y(n﹣1)+1 代入反比例函数y=﹣
中,所得的函数值记为y3…,将xn=y(n﹣1)+1 代入反比例函数y=﹣![]() 中,所得的函数值记为yn (其中n≥2,且n是整数) 如此继续下去,则在2006个函数值y1.y2,…,y2006中,值为2的情况共出现了 次?
中,所得的函数值记为yn (其中n≥2,且n是整数) 如此继续下去,则在2006个函数值y1.y2,…,y2006中,值为2的情况共出现了 次?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与x轴交于点A,与反比例函数y=![]() (x>0)的图象交于点B(2,n),过点B作BC⊥x轴于点C,点P(3n﹣4,1)是该反比例函数图象上的一点,且∠PBC=∠ABC,求反比例函数和一次函数的表达式.
(x>0)的图象交于点B(2,n),过点B作BC⊥x轴于点C,点P(3n﹣4,1)是该反比例函数图象上的一点,且∠PBC=∠ABC,求反比例函数和一次函数的表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】奥林匹克公园观光塔由五座高度不等、错落有致的独立塔组成.在综合实践活动课中,某小组的同学决定利用测角仪测量这五座塔中最高塔的高度(测角仪高度忽略不计).他们的操作方法如下:如图,他们先在B处测得最高塔塔顶A的仰角为45°,然后向最高塔的塔基直行90米到达C处,再次测得最高塔塔顶A的仰角为58°.请帮助他们计算出最高塔的高度AD约为多少米.(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)
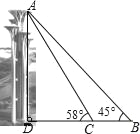
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的解析式是y=x2﹣2x﹣3.
(1)与y轴的交点坐标是 ,顶点坐标是 .
(2)在坐标系中利用描点法画出此抛物线;
x | … | … | |||||
y | … | … |
(3)结合图象回答:当﹣2<x<2时,函数值y的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我校刚刚结束的缤纷体育节上,初三年级参加了60m迎面接力比赛.假设每名同学在跑步过程中是匀速的,且交接棒的时间忽略不计,如图是A、B两班的路程差y(米)与比赛开始至A班先结束第二棒的时间x(秒)之间的函数图象.则B班第二棒的速度为_____米/秒.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,抛物线y=ax2+bx+4![]() 与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,抛物线的顶点为点D,且3OC=4OB,对称轴为直线x=
与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,抛物线的顶点为点D,且3OC=4OB,对称轴为直线x=![]() ,点E
,点E![]() ,连接CE交对称轴于点F,连接AF交抛物线于点G.
,连接CE交对称轴于点F,连接AF交抛物线于点G.
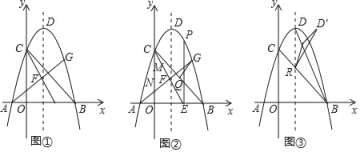
(1)求抛物线的解析式和直线CE的解析式;
(2)如图②,过E作EP⊥x轴交抛物线于点P,点Q是线段BC上一动点,当QG+![]() QB最小时,线段MN在线段CE上移动,点M在点N上方,且MN=
QB最小时,线段MN在线段CE上移动,点M在点N上方,且MN=![]() ,请求出四边形PQMN周长最小时点N的横坐标;
,请求出四边形PQMN周长最小时点N的横坐标;
(3)如图③,BC与对称轴交于点R,连接BD,点S是线段BD上一动点,将△DRS沿直线RS折叠至△D′RS,是否存在点S使得△D′RS与△BRS重叠部分的图形是直角三角形?若存在,请求出BS的长,若不存在,请说明理由.(参考数据:tan∠DBC=![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,水坝的横截面是梯形ABCD,∠ABC=37°,坝顶DC=3m,背水坡AD的坡度i(即tan∠DAB)为1:0.5,坝底AB=14m.
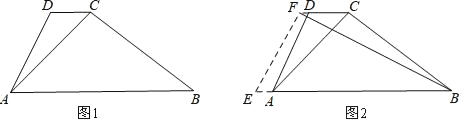
(1)求坝高;
(2)如图2,为了提高堤坝的防洪抗洪能力,防汛指挥部决定在背水坡将坝顶和坝底间时拓宽加固,使得AE=2DF,EF⊥BF,求DF的长.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com