
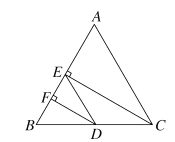
【题目】如图,在三角形ABC中,CE⊥AB于E,DF⊥AB于F,AC∥ED,CE是∠ACB的平分线,试比较∠EDF与∠BDF的大小,并说明理由.
 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AD>AB.

(1)作出∠ABC的平分线(尺规作图,保留作图痕迹,不写作法);
(2)若(1)中所作的角平分线交AD于点E,AF⊥BE,垂足为点O,交BC于点F,连接EF.求证:四边形ABFE为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂在生产过程中要消耗大量电能,消耗每千度电产生利润与电价是一次函数关系,经过测算,工厂每千度电产生利润y(元/千度))与电价x(元/千度)的函数图象如图: 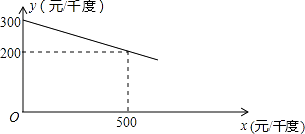
(1)当电价为600元/千度时,工厂消耗每千度电产生利润是多少?
(2)为了实现节能减排目标,有关部门规定,该厂电价x(元/千度)与每天用电量m(千度)的函数关系为x=5m+600,且该工厂每天用电量不超过60千度,为了获得最大利润,工厂每天应安排使用多少度电?工厂每天消耗电产生利润最大是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P1是一块半径为1的半圆形纸板,在P1的左下端剪去一个半径为 ![]() 的半圆后得到图形P2 , 然后依次剪去一个更小的半圆(其直径为前一个被剪掉半圆的半径)得图形P3 , P4 , …,Pn , …,记纸板Pn的面积为Sn , 试通过计算S1 , S2 , 猜想得到Sn﹣1﹣Sn=(n≥2).
的半圆后得到图形P2 , 然后依次剪去一个更小的半圆(其直径为前一个被剪掉半圆的半径)得图形P3 , P4 , …,Pn , …,记纸板Pn的面积为Sn , 试通过计算S1 , S2 , 猜想得到Sn﹣1﹣Sn=(n≥2). 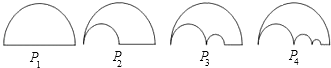
查看答案和解析>>
科目:初中数学 来源: 题型:
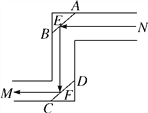
【题目】如图,潜望镜中的两个镜片AB和CD是平行的,光线经过镜子反射时,∠AEN=∠BEF,∠EFD=∠CFM,那么进入潜望镜的光线NE和离开潜望镜的光线FM是平行的吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】陈杰骑自行车去上学,当他以往常的速度骑了一段路时,忽然想起要买某本书,于是又折回到刚经过的一家书店,买到书后继续赶去学校.以下是他本次上学的路程与所用时间的关系示意图.根据图中提供的信息回答下列问题:
(1)陈杰家到学校的距离是多少米?书店到学校的距离是多少米?
(2)陈杰在书店停留了多少分钟?本次上学途中,陈杰一共行驶了多少米?
(3)在整个上学的途中哪个时间段陈杰骑车速度最快?最快的速度是多少米?
(4)如果陈杰不买书,以往常的速度去学校,需要多少分钟?本次上学比往常多用多少分钟?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若四边形中某个顶点与其它三个顶点的距离相等,则这个四边形叫做等距四边形,这个顶点叫做这个四边形的等距点.
(1)判断:一个内角为120°的菱形 等距四边形.(填“是”或“不是”)
(2)如图,在5×5的网格图中有A、B两点,请在答题卷给出的两个网格图上各找出C、D两个格点,使得以A、B、C、D为顶点的四边形为互不全等的“等距四边形”,画出相应的“等距四边形”,并写出该等距四边形的端点均为非等距点的对角线长.


端点均为非等距点的对角线长为 端点均为非等距点的对角线长为
(3)如图,已知△ABE与△CDE都是等腰直角三角形,∠AEB=∠DEC=90°,连结AD,AC ,BC,若四边形ABCD是以A为等距点的等距四边形,求∠BCD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某巡警骑摩托车在一条南北大道上巡逻,某天他从岗亭出发,晚上停留在A处,规定向北方向为正,当天行驶情况记录如下(单位:千米):+10,﹣8,+7,﹣15,+6,﹣16,+4,﹣2
(1)A处在岗亭何方?距离岗亭多远?
(2)若摩托车每行驶1千米耗油0.5升,这一天共耗油多少升?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com