
【题目】若正方形有两个相邻顶点在三角形的同一条边上,其余两个顶点分别在三角形的另两条边上,则正方形称为三角形该边上的内接正方形,△ABC中,设BC=a,AC=b,AB=c,各边上的高分别记为![]() ,
,![]() ,
,![]() ,各边上的内接正方形的边长分别记为
,各边上的内接正方形的边长分别记为![]() ,
,![]() ,
,![]() .
.
(1)模拟探究:如图,正方形EFGH为△ABC的BC边上的内接正方形,求证:![]() ;
;
(2)特殊应用:若∠BAC=90°,![]() =
=![]() =2,求
=2,求![]() 的值;
的值;
(3)拓展延伸:若△ABC为锐角三角形,b<c,请判断![]() 与
与![]() 的大小,并说明理由.
的大小,并说明理由.

【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() >
>![]() .
.
【解析】
试题分析:(1)先根据EH∥FG,判定△AEH∽△ABC,再根据相似三角形对应边成比例,列出比例式变形即可得到![]() ;
;
(2)先根据(1)中的结论得出![]() ,再将
,再将![]() =c和
=c和![]() =2代入变形,即可求得
=2代入变形,即可求得![]() 的值;
的值;
(3)先根据(1)中的结论得出![]() 和
和![]() ,变形得出
,变形得出![]() ,
,![]() ,再根据△ABC得到b
,再根据△ABC得到b![]() =c
=c![]() ,
, ![]() =csinA,
=csinA,![]() =bsinA,最后代入代数式
=bsinA,最后代入代数式![]() 进行变形推导,即可得出
进行变形推导,即可得出![]() 与
与![]() 的大小关系.
的大小关系.
试题解析:∵正方形EFGH中,EH∥FG,∴△AEH∽△ABC,∵AD⊥BC,∴![]() ,即
,即![]() ,∴
,∴![]() ;
;
(2)由(1)得:![]() ,∵∠A=90°,∴
,∵∠A=90°,∴![]() =c,又∵
=c,又∵![]() =2,∴
=2,∴![]() =
=![]() ;
;
(3)![]() >
>![]() .
.
证明:由(1)得:![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,∵S=
,∵S=![]() b
b![]() =
=![]() c
c![]() ,∴2S=b
,∴2S=b![]() =c
=c![]() ,又∵
,又∵![]() =csinA,
=csinA,![]() =bsinA,∴
=bsinA,∴![]() =
=![]() =
=![]()
=![]() ,∵b<c,sinA<1,∴
,∵b<c,sinA<1,∴![]() <0,即
<0,即![]() <0,∴
<0,∴![]() >
>![]() .
.


 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,已知点D、E、F分别为边BC、AD、CE的中点,且△ABC的面积是4cm2 , 则阴影部分面积等于( ) 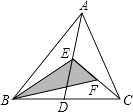
A.1cm2
B.2cm2
C.0.25cm2
D.0.5cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国某部边防军小分队成一列在野外行军,通讯员在队伍中,数了一下他前后的人数,发现前面人数是后面的两倍,他往前超了6位战士,发现前面的人数和后面的人数一样.
(1)这列队伍一共有多少名战士?
(2)这列队伍要过一座320米的大桥,为安全起见,相邻两个战士保持相同的一定间距,行军速度为5米/秒,从第一位战士刚上桥到全体通过大桥用了100秒时间,请问相邻两个战士间距离为多少米(不考虑战士身材的大小)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面对话: 小红妈:“售货员,请帮我买些梨.”
售货员:“小红妈,您上次买的那种梨都卖完了,我们还没来得及进货,我建议这次您买些新进的苹果,价格比梨贵一点,不过苹果的营养价值更高.”
小红妈:“好,你们很讲信用,这次我照上次一样,也花30元钱.”
对照前后两次的电脑小票,小红妈发现:每千克苹果的价格是梨的1.5倍,苹果的重量比梨轻2.5千克.
试根据上面对话和小红妈的发现,分别求出梨和苹果的单价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若∠A的两边与∠B的两边分别平行,且∠A的度数比∠B的度数的3倍少40°,则∠B的度数为( )
A. 20° B. 55° C. 20°或55° D. 75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】钟面角是指时钟的时针与分针所成的角.如图,图①、图②、图③三个钟面上的时刻分别记录了某中学的早晨上课时间7:30、中午放学时间11:50、下午放学时间17:00.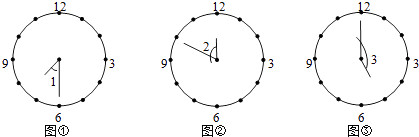
(1)分别写出图中钟面角的度数:∠1=°、∠2=°、∠3=°;
(2)在某个整点,钟面角可能会等于90°,写出可能的一个时刻为;
(3)请运用一元一次方程的知识解决问题:钟面上,在7:30~8:00之间,钟面角等于90°的时刻是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
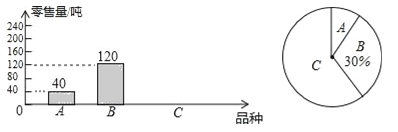
【题目】为了解茂名某水果批发市场荔枝的销售情况,某部门对该市场的三种荔枝品种A、B、C在6月上半月的销售进行调查统计,绘制成如下两个统计图(均不完整).请你结合图中的信息,解答下列问题:
(1)该市场6月上半月共销售这三种荔枝多少吨?
(2)该市场某商场计划六月下半月进货A、B、C三种荔枝共500千克,根据该市场6月上半月的销售情况,求该商场应购进C品种荔枝多少千克比较合理?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com