
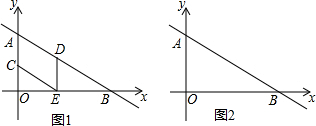
 如图,在平面直角坐标系中,直线y=-
如图,在平面直角坐标系中,直线y=-
| ||
| 3 |
| AC |
| OA |
| AD |
| AB |
| t |
| 6 |
| 12-2t |
| 12 |
| ||
| 3 |
| ||
| 3 |
| 1 |
| 2 |
| ||
| 3 |


科目:初中数学 来源: 题型:
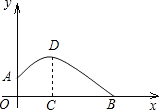 如图,一个运动员推铅球,铅球在点A处出手,出手时球离地面约1.8m.铅球落地点在B处,铅球运行中在运动员前3m处(即OC=3)达到最高点,最高点高为3.6m.已知铅球经过的路线是抛物线,根据图示的直角坐标系,你能算出该运动员的成绩吗?
如图,一个运动员推铅球,铅球在点A处出手,出手时球离地面约1.8m.铅球落地点在B处,铅球运行中在运动员前3m处(即OC=3)达到最高点,最高点高为3.6m.已知铅球经过的路线是抛物线,根据图示的直角坐标系,你能算出该运动员的成绩吗?查看答案和解析>>
科目:初中数学 来源: 题型:
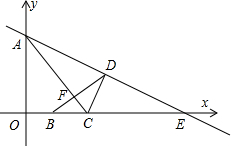 已知抛物线y=ax2+bx+8(a>
已知抛物线y=ax2+bx+8(a>| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 7 |
| 2 |
| 3 |
| 11 |
| 12 |
| 14 |
| 15 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,一个四边形纸片ABCD,∠B=∠D=90°,把纸片按如图所示折叠,使点B落在AD边上的B′点,AE是折痕,∠C=130°,则∠AEB的度数为
如图,一个四边形纸片ABCD,∠B=∠D=90°,把纸片按如图所示折叠,使点B落在AD边上的B′点,AE是折痕,∠C=130°,则∠AEB的度数为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com