
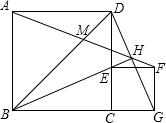
 如图,ABCD、CEFG是正方形,E在CD上,直线BE、DG交于H,且HE•HB=
如图,ABCD、CEFG是正方形,E在CD上,直线BE、DG交于H,且HE•HB=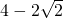 ,BD、AF交于M,当E在线段CD(不与C、D重合)上运动时,下列四个结论:①BE⊥GD;②AF、GD所夹的锐角为45°;③GD=
,BD、AF交于M,当E在线段CD(不与C、D重合)上运动时,下列四个结论:①BE⊥GD;②AF、GD所夹的锐角为45°;③GD= ;④若BE平分∠DBC,则正方形ABCD的面积为4.其中正确的结论个数有
;④若BE平分∠DBC,则正方形ABCD的面积为4.其中正确的结论个数有 BC2=BE•BH,因此只需求出BE•BH的值即可得到正方形的面积,可先求出BE、EH的比例关系,代入已知的乘积式中,即可求得BE•BH的值,由此得解.
BC2=BE•BH,因此只需求出BE•BH的值即可得到正方形的面积,可先求出BE、EH的比例关系,代入已知的乘积式中,即可求得BE•BH的值,由此得解. ,即DG=
,即DG= AM;
AM;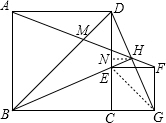
 x,EG=DE=
x,EG=DE= x,DC=BC=(
x,DC=BC=( +1)x;
+1)x; +2,即EH=
+2,即EH=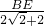 ;
;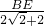 =4-2
=4-2 ,即BE•BH=4
,即BE•BH=4 ;
; ,
, BC2=4
BC2=4 ,得:BC2=4,即正方形ABCD的面积为4;
,得:BC2=4,即正方形ABCD的面积为4;

科目:初中数学 来源: 题型:
 4、如图,?ABCD中,E、F分别为AD、BC的中点,AF与BE交于点M,CE与DF交于点N,请你在图中找出三个平行四边形(?ABCD除外)
4、如图,?ABCD中,E、F分别为AD、BC的中点,AF与BE交于点M,CE与DF交于点N,请你在图中找出三个平行四边形(?ABCD除外)查看答案和解析>>
科目:初中数学 来源: 题型:
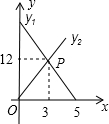 的线段y1、y2分别表示小东、小明离B地的距离(千米)与所用时间(小时)的关系.
的线段y1、y2分别表示小东、小明离B地的距离(千米)与所用时间(小时)的关系.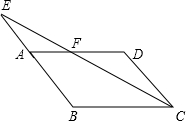
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
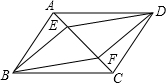 如图,?ABCD的对角线AC上两点E、F,要使四边形BEDF是平行四边形,还要添加一个条件是
如图,?ABCD的对角线AC上两点E、F,要使四边形BEDF是平行四边形,还要添加一个条件是查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•历城区一模)如图,?ABCD中,∠BCD的平分线CE交边AD于E,∠ABC的平分线BG交CE于F,交AD于G.若AB=3,BC=5,求EG的长.
(2013•历城区一模)如图,?ABCD中,∠BCD的平分线CE交边AD于E,∠ABC的平分线BG交CE于F,交AD于G.若AB=3,BC=5,求EG的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com