证明:方法①:∵AB=AC,∠B=∠C,∠A=∠A,
∴△ACD≌△ABE(ASA).
∴AD=AE.
又∵AC=AB,
∴AC-AE=AB-AD.
∴CE=BD.
方法②:连CB,
∵AB=AC,
∴∠ABC=∠ACB.
又∵∠ACD=∠ABE,
∴∠DCB=∠EBC.
在△BCD和△CBE中
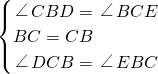
,
∴△BCD≌△CBE(ASA).
∴BD=CE.
分析:本题有两种解法:
①证△ADC≌△AEB,得AE=AD,然后根据AB=AC,得出CE=BD.
②连接BC,通过证△BEC≌△CDB来得出BD=CE的结论.
点评:此题考查简单的线段相等,可以通过全等三角形来证明,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.

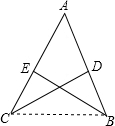
 如图,已知AB=AC,D、E分别为AB、AC上两点,∠B=∠C,求证:BD=CE.
如图,已知AB=AC,D、E分别为AB、AC上两点,∠B=∠C,求证:BD=CE.
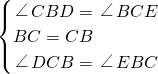 ,
,
