
ЁОЬтФПЁПШчЭМ1ЃЌжБЯпyЃНk1x+bгыЗДБШР§КЏЪ§yЃН![]() ЕФЭМЯѓНЛгкAЃЈ1ЃЌ6ЃЉЃЌBЃЈaЃЌ3ЃЉСНЕуЃЎ
ЕФЭМЯѓНЛгкAЃЈ1ЃЌ6ЃЉЃЌBЃЈaЃЌ3ЃЉСНЕуЃЎ
ЃЈ1ЃЉЧѓk1ЁЂk2ЕФжЕЃЛ
ЃЈ2ЃЉНсКЯЭМаЮЃЌдкЕквЛЯѓЯоФкЃЌжБНгаДГіk1x+bЉ![]() ЃО0ЪБЃЌxЕФШЁжЕЗЖЮЇЃЛ
ЃО0ЪБЃЌxЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЬнаЮOBCEжаЃЌBCЁЮOEЃЌЙ§ЕуCзїCEЁЭxжсгкЕуEЃЌCEКЭЗДБШР§КЏЪ§ЕФЭМЯѓНЛгкЕуPЃЌЕБЬнаЮOBCEЕФУцЛ§ЮЊ9ЪБЃЌЧыХаЖЯPCКЭPEЕФДѓаЁЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
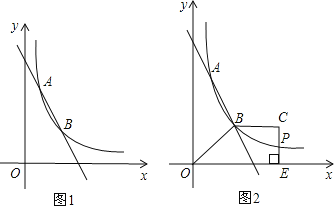
ЁОД№АИЁПЃЈ1ЃЉk1ЁЂk2ЕФжЕЗжБ№ЮЊЉ3ЃЌ6ЃЛЃЈ2ЃЉ1ЃМxЃМ2ЪБЃЌk1x+bЉ![]() ЃО0ЃЛЃЈ3ЃЉPCЃНPEЃЎРэгЩМћНтЮі.
ЃО0ЃЛЃЈ3ЃЉPCЃНPEЃЎРэгЩМћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉЯШАбAЃЈ1ЃЌ6ЃЉДњШыyЃН![]() ПЩЧѓЕУk2ЃН1ЁС6ЃН6ЃЌдйАбBЃЈaЃЌ3ЃЉДњШыyЃН
ПЩЧѓЕУk2ЃН1ЁС6ЃН6ЃЌдйАбBЃЈaЃЌ3ЃЉДњШыyЃН![]() ПЩЕУaЃН2ЃЌМДBЕузјБъЮЊЃЈ2ЃЌ3ЃЉЃЌШЛКѓАбAЃЈ1ЃЌ6ЃЉЁЂBЃЈ2ЃЌ3ЃЉДњШыyЃНk1x+bЕУЕНЙигкk1ЁЂbЕФЗНГЬзщЃЌНтЗНГЬзщМДПЩЃЛЃЈ2ЃЉЙлВьЭМЯѓЕУЕНЕБxЃМ0Лђ1ЃМxЃМ2ЪБЃЌжБЯпyЃНk1x+bЖМдкЗДБШР§КЏЪ§yЃН
ПЩЕУaЃН2ЃЌМДBЕузјБъЮЊЃЈ2ЃЌ3ЃЉЃЌШЛКѓАбAЃЈ1ЃЌ6ЃЉЁЂBЃЈ2ЃЌ3ЃЉДњШыyЃНk1x+bЕУЕНЙигкk1ЁЂbЕФЗНГЬзщЃЌНтЗНГЬзщМДПЩЃЛЃЈ2ЃЉЙлВьЭМЯѓЕУЕНЕБxЃМ0Лђ1ЃМxЃМ2ЪБЃЌжБЯпyЃНk1x+bЖМдкЗДБШР§КЏЪ§yЃН![]() ЕФЭМЯѓЩЯЗНЃЌМДk1x+bЉ
ЕФЭМЯѓЩЯЗНЃЌМДk1x+bЉ![]() ЃО0ЃЛЃЈ3ЃЉИљОнЬнаЮЕФаджЪЕУЕНBCЁЮOEЃЌдђгЩBЕузјБъЮЊЃЈ2ЃЌ3ЃЉЃЌЕУЕНCЕуЕФзнзјБъЮЊ3ЃЌЩшCЕузјБъЮЊЃЈaЃЌ3ЃЉЃЌдђEЕузјБъЮЊЃЈaЃЌ0ЃЉЃЌPЕуЕФКсзјБъЮЊaЃЌРћгУPЕудкyЃН
ЃО0ЃЛЃЈ3ЃЉИљОнЬнаЮЕФаджЪЕУЕНBCЁЮOEЃЌдђгЩBЕузјБъЮЊЃЈ2ЃЌ3ЃЉЃЌЕУЕНCЕуЕФзнзјБъЮЊ3ЃЌЩшCЕузјБъЮЊЃЈaЃЌ3ЃЉЃЌдђEЕузјБъЮЊЃЈaЃЌ0ЃЉЃЌPЕуЕФКсзјБъЮЊaЃЌРћгУPЕудкyЃН![]() ЕФЭМЯѓЩЯЃЌдђPЕузјБъЮЊЃЈaЃЌ
ЕФЭМЯѓЩЯЃЌдђPЕузјБъЮЊЃЈaЃЌ![]() ЃЉЃЌИљОнЬнаЮЕФУцЛ§ЙЋЪНЕУЕН
ЃЉЃЌИљОнЬнаЮЕФУцЛ§ЙЋЪНЕУЕН![]() ЃЈBC+OEЃЉЁСCEЃН9ЃЌМД
ЃЈBC+OEЃЉЁСCEЃН9ЃЌМД![]() ЃЈa+aЉ2ЃЉЁС3ЃН9ЃЌНтЕУaЃН4ЃЌвзЕУPCЃН3Љ
ЃЈa+aЉ2ЃЉЁС3ЃН9ЃЌНтЕУaЃН4ЃЌвзЕУPCЃН3Љ![]() ЃЌPEЃН
ЃЌPEЃН![]() Љ0ЃН
Љ0ЃН![]() ЃЌгкЪЧгаPCЃНPEЃЎ
ЃЌгкЪЧгаPCЃНPEЃЎ
ЃЈ1ЃЉАбAЃЈ1ЃЌ6ЃЉДњШыyЃН![]() ЕУЃЌk2ЃН1ЁС6ЃН6ЃЌЫљвдЗДБШР§КЏЪ§ЕФНтЮіЪНЮЊyЃН
ЕУЃЌk2ЃН1ЁС6ЃН6ЃЌЫљвдЗДБШР§КЏЪ§ЕФНтЮіЪНЮЊyЃН![]() ЃЌ
ЃЌ
АбBЃЈaЃЌ3ЃЉДњШыyЃН![]() ЕУЃЌ3ЃН
ЕУЃЌ3ЃН![]() ЃЌНтЕУaЃН2ЃЌЫљвдBЕузјБъЮЊЃЈ2ЃЌ3ЃЉЃЌ
ЃЌНтЕУaЃН2ЃЌЫљвдBЕузјБъЮЊЃЈ2ЃЌ3ЃЉЃЌ
АбAЃЈ1ЃЌ6ЃЉЁЂBЃЈ2ЃЌ3ЃЉДњШыyЃНk1x+bЕУЃЌ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌЫљвдk1ЁЂk2ЕФжЕЗжБ№ЮЊЉ3ЃЌ6ЃЛ
ЃЌЫљвдk1ЁЂk2ЕФжЕЗжБ№ЮЊЉ3ЃЌ6ЃЛ
ЃЈ2ЃЉ1ЃМxЃМ2ЪБЃЌk1x+bЉ![]() ЃО0ЃЛ
ЃО0ЃЛ
ЃЈ3ЃЉPCЃНPEЃЎРэгЩШчЯТЃК
ЁпЫФБпаЮOBDEЮЊЬнаЮЃЌ
ЁрBCЁЮOEЃЌ
ЖјBЕузјБъЮЊЃЈ2ЃЌ3ЃЉЃЌ
ЁрCЕуЕФзнзјБъЮЊ3ЃЌ
ЩшCЕузјБъЮЊЃЈaЃЌ3ЃЉЃЌ
ЁпCEЁЭxжсЃЌ
ЁрEЕузјБъЮЊЃЈaЃЌ0ЃЉЃЌPЕуЕФКсзјБъЮЊaЃЌ
ЁпPЕудкyЃН![]() ЕФЭМЯѓЩЯЃЌ
ЕФЭМЯѓЩЯЃЌ
ЁрPЕузјБъЮЊЃЈaЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЁпЬнаЮOBCEЕФУцЛ§ЮЊ9ЃЌ
Ёр![]() ЃЈBC+OEЃЉЁСCEЃН9ЃЌМД
ЃЈBC+OEЃЉЁСCEЃН9ЃЌМД![]() ЃЈa+aЉ2ЃЉЁС3ЃН9ЃЌНтЕУaЃН4ЃЌ
ЃЈa+aЉ2ЃЉЁС3ЃН9ЃЌНтЕУaЃН4ЃЌ
ЁрCЕузјБъЮЊЃЈ4ЃЌ3ЃЉЃЌPЕузјБъЮЊЃЈ4ЃЌ![]() ЃЉЃЌEЕузјБъЮЊЃЈ4ЃЌ0ЃЉЃЌ
ЃЉЃЌEЕузјБъЮЊЃЈ4ЃЌ0ЃЉЃЌ
ЁрPCЃН3Љ![]() ЃН
ЃН![]() ЃЌPEЃН
ЃЌPEЃН![]() Љ0ЃН
Љ0ЃН![]() ЃЌ
ЃЌ
ЁрPCЃНPEЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСЯТСаВФСЯЃК
ЛЗЪгЕБНёЪРНчЃЌПЦММДДаТвбГЩЮЊЗЂДяЙњМвБЃГжГжОУОКељСІЕФЁАЗЈБІЁБЃЎбаОПгыЪдбщЗЂеЙЃЈR&DЃЉЛюЖЏЕФЙцФЃКЭЧПЖШжИБъЗДгГвЛИіЕиЧјЕФПЦММЪЕСІКЭКЫаФОКељСІЃЎ
ББОЉЪадкбаОПКЭЪЕбщЗЂеЙЃЈR&DЃЉЛюЖЏжаЕФОЗбЭЖШывВдкж№ФъдіМг.2012ФъББОЉЪаШЋФъбаОПгыЪдбщЗЂеЙЃЈR&DЃЉОЗбЭЖШы1031.1вкдЊЃЌБШЩЯФъдіГЄ10.1%.2013ФъШЋФъбаОПгыЪдбщЗЂеЙЃЈR&DЃЉОЗбЭЖШы1200.7вкдЊ.2014ФъШЋФъбаОПгыЪдбщЗЂеЙЃЈR&DЃЉОЗбЭЖШы1286.6вкдЊ.2015ФъбаОПгыЪдбщЗЂеЙЃЈR&DЃЉОЗбЭЖШы1367.5вкдЊ.2016ФъбаОПгыЪдбщЗЂеЙЃЈR&DЃЉОЗбЭЖШы1479.8вкдЊЃЌЯрЕБгкЕиЧјЩњВњзмжЕЕФ5.94%ЃЎ
ЃЈвдЩЯЪ§ОнРДдДгкББОЉЪаЭГМЦОжЃЉ
ИљОнвдЩЯВФСЯНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉгУелЯпЭГМЦЭМЛђепЬѕаЮЭГМЦЭМНЋ2012Љ2016ФъББОЉЪадкбаОПКЭЪЕбщЗЂеЙЃЈR&DЃЉЛюЖЏжаЕФОЗбЭЖШыБэЪОГіРДЃЌВЂдкЭМжаБъУїЯргІЪ§ОнЃЛ
ЃЈ2ЃЉИљОнЛцжЦЕФЭГМЦЭМЬсЙЉЕФаХЯЂЃЌдЄЙР2017ФъББОЉЪадкбаОПКЭЪЕбщЗЂеЙЃЈR&DЃЉЛюЖЏжаЕФОЗбЭЖШыдМЮЊЖрЩйвкдЊЃЌаДГіФуЕФдЄЙРРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯждкЃЌЫеФўЩЬГЁНјааДйЯњЛюЖЏЃЌГіЪлвЛжжгХЛнЙКЮяПЈЃЈзЂЃКДЫПЈжЛзїЮЊЙКЮягХЛнЦОжЄВЛФмЖЅЬцЛѕПюЃЉЃЌЛЈ300дЊТђетжжПЈКѓЃЌЦОПЈПЩдкетМвЩЬГЁАДБъМлЕФ8елЙКЮя.
ЃЈ1ЃЉЙЫПЭЙКТђЖрЩйдЊН№ЖюЕФЩЬЦЗЪБЃЌТђПЈгыВЛТђПЈЛЈЧЎЯрЕШЃПдкЪВУДЧщПіЯТЙКЮяКЯЫуЃП
ЃЈ2ЃЉаЁеХвЊТђвЛЬЈБъМлЮЊ3500дЊЕФБљЯфЃЌШчКЮЙКТђКЯЫуЃПаЁеХФмНкЪЁЖрЩйдЊЧЎЃП
ЃЈ3ЃЉаЁеХАДКЯЫуЕФЗНАИЃЌАбетЬЈБљЯфТђЯТЃЌШчЙћЩЬГЁЛЙФмгЏРћ25ЃЅЃЌетЬЈБљЯфЕФНјМлЪЧЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬЕъЯњЪлвЛжжГЩБОЮЊ20дЊЕФЩЬЦЗЃЌОЕїбаЃЌЕБИУЩЬЦЗУПМўЪлМлЮЊ30дЊЪБЃЌУПЬьПЩЯњЪл200МўЃКЕБУПМўЕФЪлМлУПдіМг1дЊЃЌУПЬьЕФЯњСПНЋМѕЩй5МўЃЎ
![]() ЧѓЯњСП
ЧѓЯњСП![]() Мў
Мў![]() гыЪлМл
гыЪлМл![]() дЊ
дЊ![]() жЎМфЕФКЏЪ§БэДяЪНЃЛ
жЎМфЕФКЏЪ§БэДяЪНЃЛ
![]() ШчЙћУПЬьЕФЯњСПВЛЕЭгк150МўЃЌФЧУДЃЌЕБЪлМлЮЊЖрЩйдЊЪБЃЌУПЬьЛёШЁЕФРћШѓзюДѓЃЌзюДѓРћШѓЪЧЖрЩйЃП
ШчЙћУПЬьЕФЯњСПВЛЕЭгк150МўЃЌФЧУДЃЌЕБЪлМлЮЊЖрЩйдЊЪБЃЌУПЬьЛёШЁЕФРћШѓзюДѓЃЌзюДѓРћШѓЪЧЖрЩйЃП
![]() ИУЩЬЕъРЯАхШШаФЙЋвцЪТвЕЃЌОіЖЈДгУПЬьЕФЯњЪлРћШѓжаОшГі100дЊИјЯЃЭћЙЄГЬЃЌЮЊБЃжЄОшПюКѓУПЬьЪЃгрРћШѓВЛЕЭгк2900дЊЃЌЧыжБНгаДГіИУЩЬЦЗЪлМлЕФЗЖЮЇЃЎ
ИУЩЬЕъРЯАхШШаФЙЋвцЪТвЕЃЌОіЖЈДгУПЬьЕФЯњЪлРћШѓжаОшГі100дЊИјЯЃЭћЙЄГЬЃЌЮЊБЃжЄОшПюКѓУПЬьЪЃгрРћШѓВЛЕЭгк2900дЊЃЌЧыжБНгаДГіИУЩЬЦЗЪлМлЕФЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
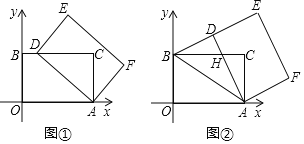
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌЫФБпаЮAOBCЪЧОиаЮЃЌЕуOЃЈ0ЃЌ0ЃЉЃЌЕуAЃЈ5ЃЌ0ЃЉЃЌЕуBЃЈ0ЃЌ3ЃЉЃЎвдЕуAЮЊжааФЃЌЫГЪБеыа§зЊОиаЮAOBCЃЌЕУЕНОиаЮADEFЃЌЕуOЃЌBЃЌCЕФЖдгІЕуЗжБ№ЮЊDЃЌEЃЌFЃЎ
ЃЈ1ЃЉШчЭМЂйЃЌЕБЕуDТфдкBCБпЩЯЪБЃЌЧѓЕуDЕФзјБъЃЛ
ЃЈ2ЃЉШчЭМЂкЃЌЕБЕуDТфдкЯпЖЮBEЩЯЪБЃЌADгыBCНЛгкЕуHЃЎ
ЂйЧѓжЄЁїADBЁеЁїAOBЃЛ
ЂкЧѓЕуHЕФзјБъЃЎ
ЃЈ3ЃЉМЧKЮЊОиаЮAOBCЖдНЧЯпЕФНЛЕуЃЌSЮЊЁїKDEЕФУцЛ§ЃЌЧѓSЕФШЁжЕЗЖЮЇЃЈжБНгаДГіНсЙћМДПЩЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
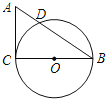
ЁОЬтФПЁПдкRtЁїACBжа,ЁЯC=90Ёу,AC=3 cm,BC=4 cm,вдBCЮЊжБОЖзїЈOНЛABгкЕуD.
(1)ЧѓЯпЖЮADЕФГЄЖШ;
(2)ЕуEЪЧЯпЖЮACЩЯЕФвЛЕу,ЪдЮЪЕБЕуEдкЪВУДЮЛжУЪБ,жБЯпEDгыЈOЯрЧа?ЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌ2ЗжБ№ЪЧФГПюРКЧђМмЕФЪЕЮяЭМгыЪОвтЭМЃЌвбжЊЕззљBC=0.60УзЃЌЕззљBCгыжЇМмACЫљГЩЕФНЧЁЯACB=75ЁуЃЌжЇМмAFЕФГЄЮЊ2.50УзЃЌРКАхЖЅЖЫFЕуЕНРКПђDЕФОрРыFD=1.35УзЃЌРКАхЕзВПжЇМмHEгыжЇМмAFЫљГЩЕФНЧЁЯFHE=60ЁуЃЌЧѓРКПђDЕНЕиУцЕФОрРыЃЈОЋШЗЕН0.01УзЃЉЃЈВЮПМЪ§ОнЃКcos75ЁуЁж0.2588ЃЌsin75ЁуЁж0.9659ЃЌtan75ЁуЁж3.732ЃЌ![]() Ёж1.732ЃЌ
Ёж1.732ЃЌ![]() Ёж1.414ЃЉ
Ёж1.414ЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЦНУцжБНЧзјБъЯЕжаЃЌвбжЊPЃЈ1ЃЌ1ЃЉЃЌCЮЊyжсе§АыжсЩЯвЛЕуЃЌDЮЊЕквЛЯѓЯоФквЛЕуЃЌЧвPCЃНPDЃЌЁЯCPDЃН90ЁуЃЌЙ§ЕуDзїжБЯпABЁЭxжсгкBЃЌжБЯпABгыжБЯпyЃНxНЛгкЕуAЃЌЧвBDЃН3ADЃЌСЌНгCDЃЌжБЯпCDгыжБЯпyЃНxНЛгкЕуQЃЌдђЕуQЕФзјБъЮЊ_____ЃЎ
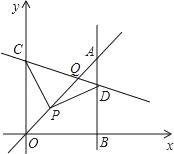
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПХзЮяЯп![]() гы
гы![]() жсНЛгкAЁЂBСНЕуЃЌЕуPдкКЏЪ§
жсНЛгкAЁЂBСНЕуЃЌЕуPдкКЏЪ§![]() ЕФЭМЯѓЩЯЃЌШєЁїPABЮЊжБНЧШ§НЧаЮЃЌдђТњзуЬѕМўЕФЕуPЕФИіЪ§ЮЊЃЈ ЃЉ.
ЕФЭМЯѓЩЯЃЌШєЁїPABЮЊжБНЧШ§НЧаЮЃЌдђТњзуЬѕМўЕФЕуPЕФИіЪ§ЮЊЃЈ ЃЉ.
A. 2Иі B. 3Иі C. 4Иі D. 6Иі
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com