
【题目】阅读下列材料:
环视当今世界,科技创新已成为发达国家保持持久竞争力的“法宝”.研究与试验发展(R&D)活动的规模和强度指标反映一个地区的科技实力和核心竞争力.
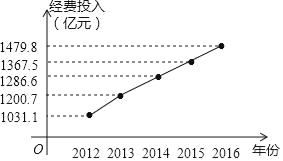
北京市在研究和实验发展(R&D)活动中的经费投入也在逐年增加.2012年北京市全年研究与试验发展(R&D)经费投入1031.1亿元,比上年增长10.1%.2013年全年研究与试验发展(R&D)经费投入1200.7亿元.2014年全年研究与试验发展(R&D)经费投入1286.6亿元.2015年研究与试验发展(R&D)经费投入1367.5亿元.2016年研究与试验发展(R&D)经费投入1479.8亿元,相当于地区生产总值的5.94%.
(以上数据来源于北京市统计局)
根据以上材料解答下列问题:
(1)用折线统计图或者条形统计图将2012﹣2016年北京市在研究和实验发展(R&D)活动中的经费投入表示出来,并在图中标明相应数据;
(2)根据绘制的统计图提供的信息,预估2017年北京市在研究和实验发展(R&D)活动中的经费投入约为多少亿元,写出你的预估理由.
【答案】(1)2012﹣2016年北京市在研究和实验发展(R&D)活动中的经费投入如图所示,见解析;(2)2017年北京市在研究和实验发展(R&D)活动中的经费投入约为1586.3亿元,理由是用近3年的平均增长率估计2017年的增长率.
【解析】
(1)画出2012﹣2016年北京市在研究和实验发展(R&D)活动中的经费投入折线图即可.
(2)设2014到2016的平均增长率为x,列出方程求出x,用近3年的平均增长率估计2017年的增长率即可解决问题.
(1)2012﹣2016年北京市在研究和实验发展(R&D)活动中的经费投入如图所示,
(2)设2014到2016的平均增长率为x,
则1286.6(1+x)2=1479.8,
解得x≈7.2%,
用近3年的平均增长率估计2017年的增长率,
则2017年北京市在研究和实验发展(R&D)活动中的经费投入约为1479.8×(1+7.2%)≈1586.3亿元,
理由是用近3年的平均增长率估计2017年的增长率.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
【题目】元旦期间,某宾馆有50个房间供游客居住,当每个房间每天的定价为180元时,房间会全部住满;当每个房间每天的定价每增加10元时,就会有一个房间空闲.如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用.
(1)若房价定为200元时,求宾馆每天的利润;
(2)房价定为多少时,宾馆每天的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,其横坐标为t,设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求以C、E、F为顶点三角形与△COD相似时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2﹣4ax(a≠0)的图象与直线y=kx+3交于点A(﹣1,![]() )、点C两点.
)、点C两点.
(1)求a,k的值;
(2)点P在第一象限的抛物线上,其横坐标为t,连接PC、PA,设△PCA的面积为S,求S关于t的函数关系式:(直接写出t的取值范围)
(3)在(2)的条件下,作CE⊥x轴于E,点P直线y=kx+3下方时,连接OP、BC交于D,连接ED,当∠ODE=90°时,求t和S的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
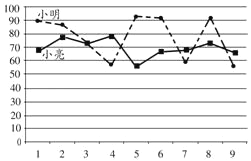
【题目】小明和小亮组成团队参加某科学比赛.该比赛的规则是:每轮比赛一名选手参加,若第一轮比赛得分满60则另一名选手晋级第二轮,第二轮比赛得分最高的选手所在团队取得胜利.为了在比赛中取得更好的成绩,两人在赛前分别作了九次测试,如图为二人测试成绩折线统计图,下列说法合理的是( )
①小亮测试成绩的平均数比小明的高;②小亮测试成绩比小明的稳定;③小亮测试成绩的中位数比小明的高;④小亮参加第一轮比赛,小明参加第二轮比赛,比较合理.
A. ①③B. ①④C. ②③D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
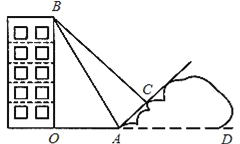
【题目】某校九年级的小红同学,在自己家附近进行测量一座楼房高度的实践活动.如图,她在山坡坡脚A出测得这座楼房的楼顶B点的仰角为60°,沿山坡往上走到C处再测得B点的仰角为45°.已知OA=200m,此山坡的坡比i=![]() ,且O、A、D在同一条直线上.
,且O、A、D在同一条直线上.
求:(1)楼房OB的高度;
(2)小红在山坡上走过的距离AC.(计算过程和结果均不取近似值)
查看答案和解析>>
科目:初中数学 来源: 题型:
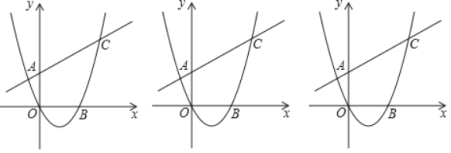
【题目】△ABC,∠A、∠B、∠C的对边分别是a、b、c,一条直线DE与边AC相交于点D,与边AB相交于点E.
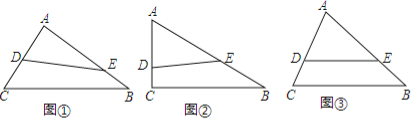
(1)如图①,若DE将△ABC分成周长相等的两部分,则AD+AE等于多少;(用a、b、c表示)
(2)如图②,若AC=3,AB=5,BC=4.DE将△ABC分成周长、面积相等的两部分,求AD;
(3)如图③,若DE将△ABC分成周长、面积相等的两部分,且DE∥BC,则a、b、c满足什么关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A、B两点.
的图象交于A、B两点.
(1)利用图中的条件,求反比例函数和一次函数的解析式.
(2)求△AOB的面积.
(3)根据图象直接写出使一次函数的值大于反比例函数的值的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
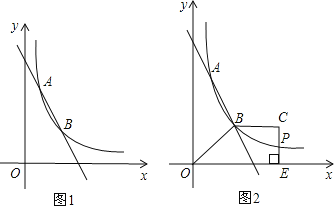
【题目】如图1,直线y=k1x+b与反比例函数y=![]() 的图象交于A(1,6),B(a,3)两点.
的图象交于A(1,6),B(a,3)两点.
(1)求k1、k2的值;
(2)结合图形,在第一象限内,直接写出k1x+b﹣![]() >0时,x的取值范围;
>0时,x的取值范围;
(3)如图2,梯形OBCE中,BC∥OE,过点C作CE⊥x轴于点E,CE和反比例函数的图象交于点P,当梯形OBCE的面积为9时,请判断PC和PE的大小关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com