练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    将抛物线y=x2向左平移6个单位，再向下平移8个单位后的抛物线为（　　）
    A、y=（x+6）2-8
    B、y=（x-6）2+8
    C、y=（x-6）2-8
    D、y=（x+6）2+8
    考点：二次函数图象与几何变换
    专题：
    分析：利用二次函数平移规律，左加右减，上加下减得出即可．
    解答：解：将抛物线y=x2向左平移6个单位，得到：y=（x+6）2，
    再向下平移8个单位后的抛物线为：y=（x+6）2-8．
    故选：A．
    点评：此题主要考查了二次函数平移变换，正确记忆平移规律是解题关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图，在梯形ABCD中，AD∥BC，将腰AB沿底BC平移至DM，若点M恰好是BC的中点，那么点N是DM的中点吗？写出你的结论并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

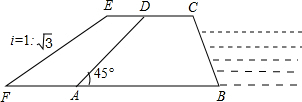    如图，某防洪指挥部发现长江边一处长100米，高8米，背水坡的坡角为45°的防洪大堤（横断面为梯形ABCD）急需加固．经调查论证，防洪指挥部专家组制定的加固方案是：沿背水坡面用土石进行加固，并使上底加宽3米，加固后背水坡EF的坡比i=1：
    		3
    ．
    （1）求加固后坝底增加的宽度AF；
    （2）求完成这项工程需要土石多少立方米？（结果保留根号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

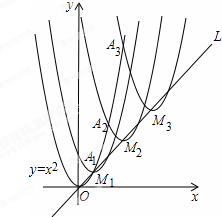    如图，抛物线y=x2在第一象限内经过的整数点（横坐标、纵坐标都为整数的点）依次为A1，A2，A3…An，…．将抛物线y=x2沿直线L：y=x向上平移，得一系列抛物线，且满足下列条件：
    ①抛物线的顶点M1，M2，M3，…Mn，…都在直线L：y=x上；
    ②抛物线依次经过点A1，A2，A3…An，…．
    则顶点M2014的坐标为（　　）
    A、（2013，2013）
    B、（2014，2014）
    C、（4027，4027）
    D、（4028，4028）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    钟表上的时间是2时30分，此时时针与分针所成的夹角是
     
    度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    二次函数y=x2的图象向左平移2个单位，得到新的图象的二次函数表达式是（　　）
    A、y=x2+2
    B、y=（x+2）2
    C、y=（x-2）2
    D、y=x2-2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

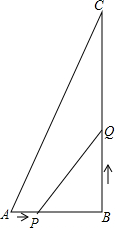    如图所示，在△ABC中，∠B=90°，△ABC三边长为整数且两直角边的长为关于x的一元二次方程x2-7x+（2k+8）=0的两实数根，其中k为正整数，且AB＜BC．
    （1）求△ABC的三边长；
    （2）点P从A点开始沿AB边向点B以1个单位长/秒的速度移动，而点Q从B点开始沿BC边向C以2个单位长/秒的速度移动，如果P，Q分别从A，B同时出发，经过几秒钟，△PBQ的面积为△ABC面积的
    1
    3
    ？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

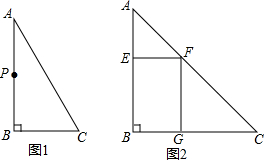    【问题发现】
    （1）如图①，△ABC为直角三角形，∠B=90°，P是边AB上任意一点（不写A、B重合），请你在△ABC的边长找另一点Q，使得S△BCP=S△BCQ，并简要说明方法；
    （2）如图②，△ABC为等腰三角形，∠B=90°，AB=10，F是边AC上任意一点（不与A、C重合），EF⊥AB，FG⊥BC，试判断图中△AEF、△CGF、四边形BEFG的具体形状；（直接写出答案）．
    【问题探究】
    （3）在（2）的条件下研究：F在边长AC上移动时，四边形BEFG的周长是否发生改变，并说明理由；（不妨设AE=x）
    （4）在（2）的条件下研究：F在边AC上移动时，四边形BEFG的面积是否存在最大值？若存在，求出来；若不存在，说明理由．（提示：我们知道完全平方式具有非负性，即（a+b）2≥0，显然（a+b）2有最小值．例如：对于y=x2+2x+2=（x+1）2+1≥1，那么y有最小值1）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    先化简，再求值：5（3a2b-ab2）-4（-ab2+3a2b），其中a=
    1
    2
    ，b=-1．

    查看答案和解析>>

    同步练习册答案