
【题目】如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒,当t为___________时,△ACP是等腰三角形.

【答案】3s
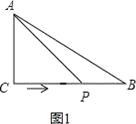
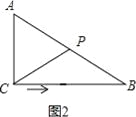
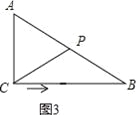
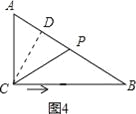
【解析】试题分析:根据题意分四种情况,针对每种情况画出相应的图形,求出相应的时间t的值即可解答本题.第一种情况:当AC=CP时,△ACP是等腰三角形,如图1所示,∵在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,∴CP=6cm,∴t=6÷2=3秒;第二种情况:当CP=PA时,△ACP是等腰三角形,如图2所示,∵在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,∴AB=10cm,∠PAC=∠PCA,∴∠PCB=∠PBC,∴PA=PC=PB=5cm,∴t=(CB+BP)÷2=(8+5)÷2=6.5秒;第三种情况:当AC=AP时,△ACP是等腰三角形,如图3所示,∵在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,∴AP=6cm,AB=10cm,∴t=(CB+BA﹣AP)÷2=(8+10﹣6)÷2=6秒;第四种情况:当AC=CP时,△ACP是等腰三角形,如图4所示,作CD⊥AB于点D,∵∠ACB=90°,AC=6cm,BC=8cm,tan∠A=![]() ,∴
,∴![]() ,AB=10cm,设CD=4a,则AD=3a,∴(4a)2+(3a)2=62,解得,a=
,AB=10cm,设CD=4a,则AD=3a,∴(4a)2+(3a)2=62,解得,a=![]() ,∴AD=3a=
,∴AD=3a=![]() ,∴t=
,∴t=![]() =7.2s.
=7.2s.
故答案为:3,6或6.5或7.2.


科目:初中数学 来源: 题型:
【题目】下列命题错误的个数有( )
①经过三个点一定可以作一个圆; ②三角形的外心到三角形各顶点的距离相等;
③同圆或等圆中,相等的圆心角所对的弧相等;④平分弦的直径垂直于弦.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
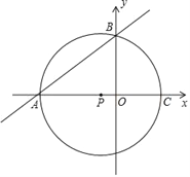
【题目】如图,点A的坐标为(﹣8,0),点P的坐标为(-![]() ,0),直线y=
,0),直线y=![]() x+b过点A,交y轴于点B,以点P为圆心,以PA为半径的圆交x轴于点C.
x+b过点A,交y轴于点B,以点P为圆心,以PA为半径的圆交x轴于点C.
(1)判断点B是否在⊙P上?说明理由.
(2)求过A、B、C三点的抛物线的解析式;并求抛物线与⊙P另外一个交点为D的坐标.
(3)⊙P上是否存在一点Q,使以A、P、B、Q为顶点的四边形是菱形?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,为了山更绿、水更清,某区大力实施生态修复工程,发展林业产业,确保到2021年实现全区森林覆盖率达到72.6%的目标.已知该区2019年全区森林覆盖率为60%,设从2019年起该区森林覆盖率年平均增长率为x,则x=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a、b、c是△ABC的三边长,且方程a(1+x2)+2bx﹣c(1﹣x2)=0的两根相等,则△ABC为( )
A. 等腰三角形 B. 直角三角形 C. 等边三角形 D. 任意三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对面积为1的△ABC逐次进行以下操作:第一次操作,分别延长AB,BC,CA至点A1 , B1 , C1 , 使得A1B=2AB,B1C=2BC,C1A=2CA,顺次连接A1 , B1 , C1 , 得到△A1B1C1 , 记其面积为S1;第二次操作,分别延长A1B1 , B1C1 , C1A1至点A2 , B2 , C2 , 使得A2B1=2A1B1 , B2C1=2B1C1 , C2A1=2C1A1 , 顺次连接A2 , B2 , C2 , 得到△A2B2C2 , 记其面积为S2 , 则S2=。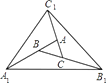
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BD平分∠ABC,点F在AB上,点G在AC上,连接FG、FC,FC与BD相交于点H,如果∠GFH与∠BHC互补.求证:∠1=∠2.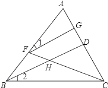
查看答案和解析>>
科目:初中数学 来源: 题型:
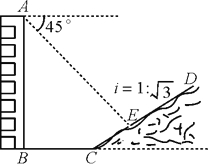
【题目】如图,一楼房AB后有一假山,其坡度为i=1∶![]() ,山坡坡面上E点处有一休息亭,测
,山坡坡面上E点处有一休息亭,测
得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角
为45°,求楼房AB的高.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com