
分析 先由②③得出y+2z=1996,借助y>z>663,求出z的值,再结合②求出x,y即可.
解答 解:$\left\{\begin{array}{l}{x>y>z>663①}\\{x+y+z=1998②}\\{2x+3y+4z=5992③}\end{array}\right.$,
③-②×2,得,y+2z=5992-1998×2=1996,
∵y>z>663,
∴3z<1996,
∴z<665$\frac{1}{3}$,
∵z>663,且为正整数,
∴z=664,或z=665;
∵y+2z=1996④,x+y+z=1998,
当z=664时,y=668,x=666(舍)
当z=665时,y=666,x=667;
故答案为:(667,666,665);
点评 此题是三元一次不定方程,主要考查了解字母细数的方程组的方法,不等式的性质,解本题的关键是得出y+2z=1996.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:解答题
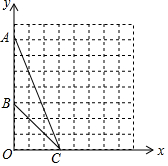 如图,在平面直角坐标系xOy中,点A的坐标为(0,7),点B的坐标为(0,3),点C的坐标为(3,0).
如图,在平面直角坐标系xOy中,点A的坐标为(0,7),点B的坐标为(0,3),点C的坐标为(3,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCED的外部时,则∠A与∠1和∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( )
如图,把△ABC纸片沿DE折叠,当点A落在四边形BCED的外部时,则∠A与∠1和∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( )| A. | 2∠A=∠2-∠1 | B. | 3∠A=2(∠2-∠1) | C. | 3∠A=2∠1-∠2 | D. | ∠A=∠2-∠1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AD是角平分线,E是AB上一点,AE=AC,EF∥BC交AC于F.下列结论①△ADC≌△ADE;②CE平分∠DEF;③AD垂直平分CE.其中正确的是( )
如图,AD是角平分线,E是AB上一点,AE=AC,EF∥BC交AC于F.下列结论①△ADC≌△ADE;②CE平分∠DEF;③AD垂直平分CE.其中正确的是( )| A. | ①②③ | B. | ① | C. | ② | D. | ③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一次函数的图象经过点(-2,12)和(3,-3).
一次函数的图象经过点(-2,12)和(3,-3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com