
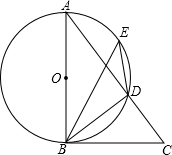
 如图,AB是⊙O的直径,点E是
如图,AB是⊙O的直径,点E是 |
| AD |
| BC |
| CA |
| CD |
| BC |
| 10 |
| BC |
| CA |
| CD |
| BC |
| 10 |


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
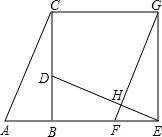 如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DE、FG相交于点H.
如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DE、FG相交于点H.查看答案和解析>>
科目:初中数学 来源: 题型:
| 时间段 | 频数 | 频率 |
| 29分钟及以下 | 108 | 0.54 |
| 30-39分钟 | 24 | 0.12 |
| 40-49分钟 | m | 0.15 |
| 50-59分钟 | 18 | 0.09 |
| 1小时及以上 | 20 | 0.1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com