
| b |
| a |
| c |
| a |


科目:初中数学 来源: 题型:
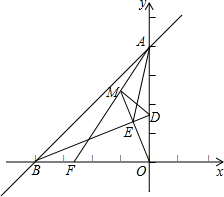 在直线y=x+4与坐标轴交于A、B两点,BD平分∠ABO,交y轴于D,OE⊥BD交AB于E点,点F在OB上,且OF=AE,AF与OE相交于M点.求证:
在直线y=x+4与坐标轴交于A、B两点,BD平分∠ABO,交y轴于D,OE⊥BD交AB于E点,点F在OB上,且OF=AE,AF与OE相交于M点.求证:查看答案和解析>>
科目:初中数学 来源: 题型:
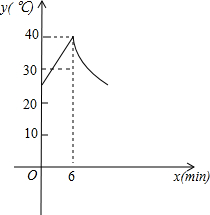 墨墨在妈妈生日当天购买了一个足浴盆作为生日礼物送给妈妈.墨墨妈妈在使用该足浴盆泡脚时,最初注入的水的温度是25℃,加热6min后,水温达到最高温度40℃,然后该足浴盆自动停止加热进行保温,设定保温过程中,水温的最低温度不低于30℃,当水温降至30℃时,该足浴盆又会再次自动加热,以此循环.加热时,温度y(℃)与时间x(min)成一次函数关系;保温时,温度y(℃)与时间x(min)成反比例函数关系,第一个加热和保温过程如图所示.
墨墨在妈妈生日当天购买了一个足浴盆作为生日礼物送给妈妈.墨墨妈妈在使用该足浴盆泡脚时,最初注入的水的温度是25℃,加热6min后,水温达到最高温度40℃,然后该足浴盆自动停止加热进行保温,设定保温过程中,水温的最低温度不低于30℃,当水温降至30℃时,该足浴盆又会再次自动加热,以此循环.加热时,温度y(℃)与时间x(min)成一次函数关系;保温时,温度y(℃)与时间x(min)成反比例函数关系,第一个加热和保温过程如图所示. 查看答案和解析>>
科目:初中数学 来源: 题型:
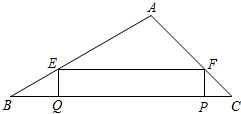 如图,在△ABC中,AB=20cm,AC=10
如图,在△ABC中,AB=20cm,AC=10 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 有六张完全相同的卡片,分A,B两组,每组三张,在A组的卡片上分别画上“√,×,√”,在B组的卡片上分别画上“√,×,×”,如图1所示.
有六张完全相同的卡片,分A,B两组,每组三张,在A组的卡片上分别画上“√,×,√”,在B组的卡片上分别画上“√,×,×”,如图1所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com