
 如图,菱形ABCD的边长为6,M、N分别是边BC、CD上的点,且MC=2MB,ND=2NC,点P是对角线BD上一点,则PM+PN的最小值是6.
如图,菱形ABCD的边长为6,M、N分别是边BC、CD上的点,且MC=2MB,ND=2NC,点P是对角线BD上一点,则PM+PN的最小值是6. 分析 作M关于BD的对称点M′交AB于M′,连接M′N交BD于P,则M′N=PM+PN的最小值,根据平行四边形的判定定理得到四边形BCNM′是平行四边形,得到M′N=BC=6,于是得到结论.
解答 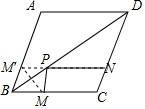 解:作M关于BD的对称点M′交AB于M′,连接M′N交BD于P,
解:作M关于BD的对称点M′交AB于M′,连接M′N交BD于P,
则M′N=PM+PN的最小值,
∵MC=2MB,ND=2NC,
∴BM=CN=2,
∴BM′=2,
∴BM′=CN,
∵BM′∥CN,
∴四边形BCNM′是平行四边形,
∴M′N=BC=6,
∴PM+PN的最小值=6,
故答案为:6.
点评 本题考查的是轴对称-最短路线问题及菱形的性质和勾股定理的运用,熟知两点之间线段最短的知识是解答此题的关键.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题
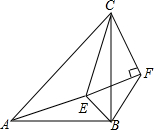 如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.
如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
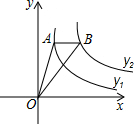 如图,反比例函数y1=$\frac{k}{x}$(0<k<3,x>0)与y2=$\frac{3}{x}$(x>0)的图象如图所示,反比例函数y1的图象上有一点A,其横坐标为a,过点A作x轴的平行线交反比例函数y2的图象于点B,连接AO、BO,若△ABO的面积为S,则S关于a的大致函数图象是( )
如图,反比例函数y1=$\frac{k}{x}$(0<k<3,x>0)与y2=$\frac{3}{x}$(x>0)的图象如图所示,反比例函数y1的图象上有一点A,其横坐标为a,过点A作x轴的平行线交反比例函数y2的图象于点B,连接AO、BO,若△ABO的面积为S,则S关于a的大致函数图象是( )| A. |  | B. | 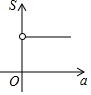 | C. | 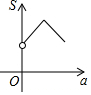 | D. | 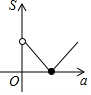 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
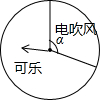 为抵制乐天,吸引顾客,某商场进行一个有奖销售的促销活动,设立了一个可以自由转动的转盘,并规定,顾客购物200元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品(若指针落在两个区域的交界处,则重新转动转盘).下表是此次促销活动中的一组统计数据:
为抵制乐天,吸引顾客,某商场进行一个有奖销售的促销活动,设立了一个可以自由转动的转盘,并规定,顾客购物200元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品(若指针落在两个区域的交界处,则重新转动转盘).下表是此次促销活动中的一组统计数据:| 转动转盘的次数n | 100 | 200 | 400 | 500 | 800 | 1000 |
| 落在“可乐”区域的次数m | 72 | 142 | 278 | 355 | b | 701 |
| 落在“可乐”区域的频率$\frac{m}{n}$ | 0.72 | 0.71 | 0.695 | a | 0.705 | 0.701 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
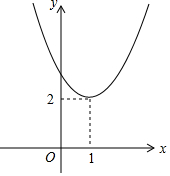 “爱心是人间真情所在”!现用“?”定义一种运算,对任意实数m、n和抛物线y=ax2,当y=ax2?(m,n)后都可得到y=a(x-m)2+n.当y=x2?(m,n)后得到了新函数的图象(如图所示),则nm=2.
“爱心是人间真情所在”!现用“?”定义一种运算,对任意实数m、n和抛物线y=ax2,当y=ax2?(m,n)后都可得到y=a(x-m)2+n.当y=x2?(m,n)后得到了新函数的图象(如图所示),则nm=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com