练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在△ABC中，AB=AC，AB的垂直平分线MN交AC于D点．若BD平分∠ABC，则∠A=°．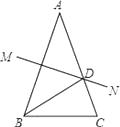

    【答案】36
    【解析】∵MN垂直平分AB，
    ∴AD=BD
    ∠A=∠ABD
    又BD平分∠ABC
    ∴∠ABD=CBD
    ∵AB=AC
    ∴∠ABC=∠ACB
    设∠A为x，则∠ABD=CBD=∠A=x,∠ABC=∠ACB=2x;由三角形内角和得
    ∠A+∠ABC+∠ACB=180°
    即x+2x+2x=180°
    x=36°
    ∴∠A=36°


    【考点精析】根据题目的已知条件，利用线段垂直平分线的性质的相关知识可以得到问题的答案，需要掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】下列多边形中，内角和与外角和相等的是（ ）
    A.四边形
    B.五边形
    C.六边形
    D.八边形

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】据河南省发改委发布消息，2016年全省固定资产投资继续保持持续稳定增长，全年完成39753亿元，总量居全国第3位．将数据39753亿用科学记数法表示为（ ）
    A.3.9753×109
    B.0.39753×1010
    C.39.753×1011
    D.3.9753×1012

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某水电站兴建了一个最大蓄水容量为12万米3的蓄水池，并配有2个流量相同的进水口和1个出水口．某天从0时至12时，进行机组试运行.其中，0时至2时打开2个进水口进水；2时，关闭1个进水口减缓进水速度，至蓄水池中水量达到最大蓄水容量后，随即关闭另一个进水口，并打开出水口，直至12时蓄水池中的水放完为止.
    若这3个水口的水流都是匀速的，且2个进水口的水流速度一样，水池中的蓄水量 y（万米3）与时间t（时）之间的关系如图所示，请根据图象解决下列问题：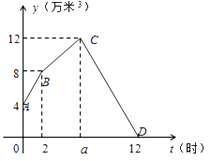

    （1）蓄水池中原有蓄水万米3 ， 蓄水池达最大蓄水量12万米3的时间a的值为；
    （2）求线段BC、CD所表示的y与t之间的函数关系式；
    （3）蓄水池中蓄水量维持在m万米3以上（含m万米3）的时间有3小时，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】【探索发现】

    如图①，是一张直角三角形纸片，∠B=60°，小明想从中剪出一个以∠B为内角且面积最大的矩形，经过多次操作发现，当沿着中位线DE、EF剪下时，所得的矩形的面积最大，随后，他通过证明验证了其正确性，并得出：矩形的最大面积与原三角形面积的比值为 ．

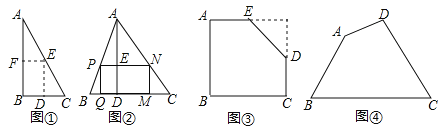
    【拓展应用】

    如图②，在△ABC中，BC=a，BC边上的高AD=h，矩形PQMN的顶点P、N分别在边AB、AC上，顶点Q、M在边BC上，则矩形PQMN面积的最大值为 ．（用含a，h的代数式表示）

    【灵活应用】

    如图③，有一块“缺角矩形”ABCDE，AB=32，BC=40，AE=20，CD=16，小明从中剪出了一个面积最大的矩形（∠B为所剪出矩形的内角），求该矩形的面积．

    【实际应用】

    如图④，现有一块四边形的木板余料ABCD，经测量AB=50cm，BC=108cm，CD=60cm，且tanB=tanC=，木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN，求该矩形的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】现定义运算“★”，对于任意实数a，b，都有a★b=a2﹣a×b+b，如：3★5=32﹣3×5+5，若x★2=10，则实数x的值为（ ）
    A.﹣4或﹣l
    B.4或﹣l
    C.4或﹣2
    D.﹣4或2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】
    （1）已知：如图1，等腰直角三角形ABC中，∠B=90°，AD是∠BAC的外角平分线，交CB边的延长线于点D．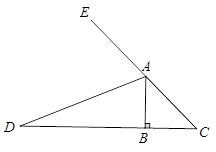
    图1
    求证：BD=AB+AC
    （2）对于任意三角形ABC，∠ABC=2∠C，AD是∠BAC的外角平分线，交CB边的延长线于点D，如图2，请你写出线段AC、AB、BD之间的数量关系并加以证明．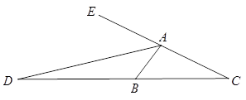

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在同一坐标系中，函数y=kx与y=x﹣k的图象大致是（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列命题是真命题的是（ ）
    A.如果 =1，那么a=1；
    B.三个内角分别对应相等的两个三角形全等；
    C.如果a是有理数，那么a是实数 ；
    D.两边一角对应相等的两个三角形全等。

    查看答案和解析>>

    同步练习册答案