
分析 (1)由四边形四个点的坐标易得OA=BC=5,BC∥OA,以OA为直径作⊙D,与直线BC分别交于点E、F,根据圆周角定理得∠OEA=∠OFA=90°,如图1,作DG⊥EF于G,连DE,则DE=OD=2.5,DG=2,根据垂径定理得EG=GF,接着利用勾股定理可计算出EG=1.5,于是得到E(1,2),F(4,2),即点P在E点和F点时,满足条件,此时,当$\left\{\begin{array}{l}{m-5≤4}\\{m≥1}\end{array}\right.$,即1≤m≤9时,边BC上总存在这样的点P,使∠OPA=90°;
(2)如图2,先判断四边形OABC是平行四边形,再利用平行线的性质和角平分线定义可得到∠AQO=90°,以OA为直径作⊙D,与直线BC分别交于点E、F,则∠OEA=∠OFA=90°,于是得到点Q只能是点E或点F,当Q在F点时,证明F是BC的中点.而F点为 (4,2),得到m的值为6.5;当Q在E点时,同理可求得m的值为3.5.
解答 解:(1)存在.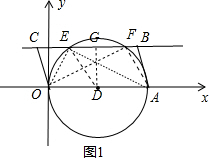
∵O(0,0)、A(5,0)、B(m,2)、C(m-5,2).
∴OA=BC=5,BC∥OA,
以OA为直径作⊙D,与直线BC分别交于点E、F,则∠OEA=∠OFA=90°,如图1,
作DG⊥EF于G,连DE,则DE=OD=2.5,DG=2,EG=GF,
∴EG=$\sqrt{D{E}^{2}-D{G}^{2}}$=1.5,
∴E(1,2),F(4,2),
∴当$\left\{\begin{array}{l}{m-5≤4}\\{m≥1}\end{array}\right.$,即1≤m≤9时,边BC上总存在这样的点P,使∠OPA=90°;
(2)如图2,
∵BC=OA=5,BC∥OA,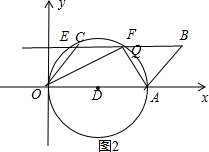 ∴四边形OABC是平行四边形,
∴四边形OABC是平行四边形,
∴OC∥AB,
∴∠AOC+∠OAB=180°,
∵OQ平分∠AOC,AQ平分∠OAB,
∴∠AOQ=$\frac{1}{2}$∠AOC,∠OAQ=$\frac{1}{2}$∠OAB,
∴∠AOQ+∠OAQ=90°,
∴∠AQO=90°,
以OA为直径作⊙D,与直线BC分别交于点E、F,则∠OEA=∠OFA=90°,
∴点Q只能是点E或点F,
当Q在F点时,∵OF、AF分别是∠AOC与∠OAB的平分线,BC∥OA,
∴∠CFO=∠FOA=∠FOC,∠BFA=∠FAO=∠FAB,
∴CF=OC,BF=AB,
而OC=AB,
∴CF=BF,即F是BC的中点.
而F点为(4,2),则$\frac{m+m-5}{2}$=4,解得m=6.5
∴此时m的值为6.5,
当Q在E点时,同理可得$\frac{m+m-5}{2}$=1,此时m的值为3.5,
综上所述,m的值为3.5或6.5.
点评 本题考查了圆的综合题:熟练掌握垂径定理、圆周角定理和平行四边形的判定与性质;理解坐标与图形性质;会利用勾股定理计算线段的长.


科目:初中数学 来源: 题型:选择题
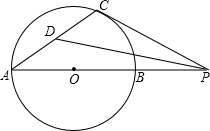 已知AB是⊙O的直径,点P是AB延长线上的一个动点,过P作⊙O的切线,切点为C,∠APC的平分线交AC于点D.若∠CPD=20°,则∠CAP等于( )
已知AB是⊙O的直径,点P是AB延长线上的一个动点,过P作⊙O的切线,切点为C,∠APC的平分线交AC于点D.若∠CPD=20°,则∠CAP等于( )| A. | 30° | B. | 20° | C. | 45° | D. | 25° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
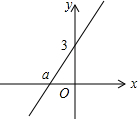 如图,直线y=kx+b与y轴交于点(0,3)、与x轴交于点(a,0),当a满足-3≤a<0时,k的取值范围是( )
如图,直线y=kx+b与y轴交于点(0,3)、与x轴交于点(a,0),当a满足-3≤a<0时,k的取值范围是( )| A. | -1≤k<0 | B. | 1≤k≤3 | C. | k≥1 | D. | k≥3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
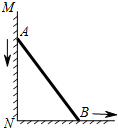 如图,一根长为5米的竹竿AB斜立于墙MN的右侧,底端B与墙角N 的距离为3米,当竹竿顶端A下滑x米时,底端B便随着向右滑行y米,反映y与x变化关系的大致图象是( )
如图,一根长为5米的竹竿AB斜立于墙MN的右侧,底端B与墙角N 的距离为3米,当竹竿顶端A下滑x米时,底端B便随着向右滑行y米,反映y与x变化关系的大致图象是( )| A. | 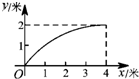 | B. | 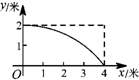 | C. | 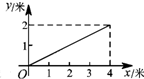 | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com