分析:(1)把x
3-10x进行因式分解,然后由x
2+3x-1=0,即可求出原式的值,(2)根据a
4+b
4+c
4-2(a
2b
2+b
2c
2+c
2a
2)=(a
2-b
2-c
2)
2-4b
2c
2,再次因式分解可得(a+b-c)(a-b+c)(a+b+c)(a-b-c),结合b+c-a=2+
,c+a-b=4-
,a+c-c=
-2,即可求出原式的值,(3)分别求出当q=1和q≠1时,前四项的和的值.
解答:解:(1)x
3-10x=x(x
2-10)=x(1-3x-10)=-3(x
2+3x)=-3,故(1)正确;
(2)a
4+b
4+c
4-2(a
2b
2+b
2c
2+c
2a
2)=(a
2-b
2-c
2)
2-4b
2c
2=(a
2-b
2-c
2+2bc)(a
2-b
2-c
2-2bc)
=(a+b-c)(a-b+c)(a+b+c)(a-b-c)
又知b+c-a=2+
,c+a-b=4-
,a+b-c=
-2,可得a+b+c=4+
,
故a
4+b
4+c
4-2(a
2b
2+b
2c
2+c
2a
2)=-11,故(2)正确;
(3)当q=1时,a
1+a
2+a
3+a
4=4a
1,当q≠1时,a
1+a
2+a
3+a
4=
,故(3)正确,
正确的有3个,故选D.
点评:本题主要考查因式定理与综合除法和完全平方式的知识点,解答本题的关键是对等式进行合理的变形,此题难度不大.



 (2012•宁德质检)如图,点A、D、B、E在同一条直线上,BC∥EF,AC=DF,∠C=∠F,请你从以下三个判断①BC=EF;②AC∥DF;③AD=DE中选择一个正确的结论,并加以证明.
(2012•宁德质检)如图,点A、D、B、E在同一条直线上,BC∥EF,AC=DF,∠C=∠F,请你从以下三个判断①BC=EF;②AC∥DF;③AD=DE中选择一个正确的结论,并加以证明. ,c+a-b=4-
,c+a-b=4- ,a+b-c=
,a+b-c= -2,则a4+b4+c4-2(a2b2+b2c2+c2a2)=-11
-2,则a4+b4+c4-2(a2b2+b2c2+c2a2)=-11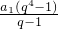 (q≠1)
(q≠1)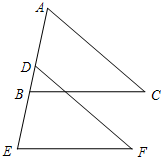 如图,点A、D、B、E在同一条直线上,BC∥EF,AC=DF,∠C=∠F,请你从以下三个判断①BC=EF;②AC∥DF;③AD=DE中选择一个正确的结论,并加以证明.
如图,点A、D、B、E在同一条直线上,BC∥EF,AC=DF,∠C=∠F,请你从以下三个判断①BC=EF;②AC∥DF;③AD=DE中选择一个正确的结论,并加以证明.