练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作BC的平行线交BE的延长线于点F，连接CF．

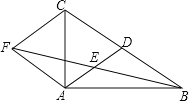
    求证：（1）AF=CD；

    （2）∠AFC=∠CDA．

    【答案】证明见解析

    【解析】

    试题分析：（1）根据AAS证△AFE≌△DBE，推出AF=BD，即可得出答案；

    （2）得出四边形ADCF是平行四边形，根据平行四边形的性质即可得到结论．

    （1）证明：∵AF∥BC，

    ∴∠AFE=∠DBE，

    ∵E是AD的中点，AD是BC边上的中线，

    ∴AE=DE，BD=CD，

    在△AFE和△DBE中

    ∴△AFE≌△DBE（AAS），

    ∴AF=BD，

    ∴AF=DC．

    （2）证明：AF∥BC，AF=DC，

    ∴四边形ADCF是平行四边形，

    ∴∠AFC=∠CDA．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】 不能判定两直线平行的条件是（ ）

    A. 同位角相等 B. 内错角相等

    C. 同旁内角相等 D. 都和第三条直线平行

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】设

    （1）请用含n的代数式表示（n为自然数）；

    （2）探究是否为4的倍数，证明你的结论并用文字描述该结论；

    （3）若一个数的算术平方根是一个自然数，则称这个数是“完全平方数”（如：1，16等），试写出这些数中，前4个“完全平方数”。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，某足球运动员站在点O处练习射门，将足球从离地面0.5m的A处正对球门踢出（点A在y轴上），足球的飞行高度y（单位：m）与飞行时间t（单位：s）之间满足函数关系y=at2+5t+c，已知足球飞行0.8s时，离地面的高度为3.5m．

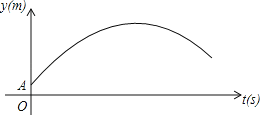
    （1）足球飞行的时间是多少时，足球离地面最高？最大高度是多少？

    （2）若足球飞行的水平距离x（单位：m）与飞行时间t（单位：s）之间具有函数关系x=10t，已知球门的高度为2.44m，如果该运动员正对球门射门时，离球门的水平距离为28m，他能否将球直接射入球门？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是⊙O的直径，OA=1，AC是⊙O的弦，过点C的切线交AB的延长线于点D，若BD=﹣1，则∠ACD= °．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果点P（a﹣4，a）在y轴上，则点P的坐标是( )

    A. (4，0) B. (0，4） C. (﹣4，0) D. (0，﹣4)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知△ABC中，AB=BC，以AB为直径的圆O交AC于点D，过点D作DE⊥BC，垂足为E，连接OE．

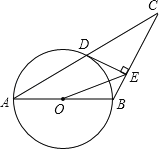
    （1）求证：DE是⊙O的切线；

    （2）若CD=，∠ACB=30°，求OE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】本学期的五次数学测试中，甲、乙两同学的平均成绩一样，方差分别为1.2、0.5，则下列说法正确的是（ ）

    A. 乙同学的成绩更稳定 B. 甲同学的成绩更稳定

    C. 甲、乙两位同学的成绩一样稳定 D. 不能确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】4是_____的算术平方根．

    查看答案和解析>>

    同步练习册答案