
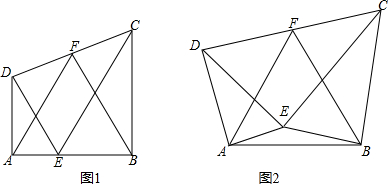
分析 (1)△ABF是等边三角形,先证明△ADF≌△GCF,再由△ADE∽△BCE得$\frac{EB}{AE}$=$\frac{BC}{AD}$=$\frac{BC}{CG}$,得CE∥AG,由此即可证明.
(2)结论不变,延长AF到G使得FG=AF,连接BG、AB,由△GCB∽△AEB,∠GBC=∠ABE,$\frac{AB}{BG}$=$\frac{EB}{BC}$得∠ABG=∠EBC=90°,再证明△ABG∽△EBC即可解决问题.
解答 (1)结论:△ABF是等边三角形.
证明:如图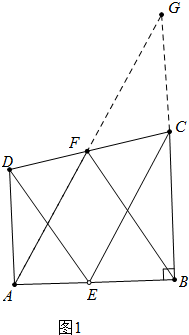 延长AF、BC交于点G.
延长AF、BC交于点G.
∵∠DAE=∠CBE=90°,
∴∠DAE+∠CBE=180°,
∴AD∥BG,
∴∠ADF=∠GCF,
在△ADF和△GCF中,
$\left\{\begin{array}{l}{∠ADF=∠GCF}\\{∠DFC=∠GFC}\\{DF=FC}\end{array}\right.$,
∴△ADF≌△GCF,
∴AF=FG,AD=CG,
∵∠ABG=90°,
∴FB=AF=FG,
∵∠DAE=∠CBE,∠DEA=∠CEB=60°,
∴△ADE∽△BCE,
∴$\frac{EB}{AE}$=$\frac{BC}{AD}$=$\frac{BC}{CG}$,
∴EC∥AG,
∴∠GAB=∠CEB=60°,
∵FA=FB,
∴△FAB是等边三角形.
(2)结论不变.
证明:如图2中,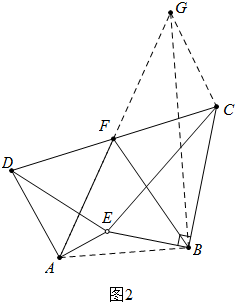 延长AF到G使得FG=AF,连接BG、AB.
延长AF到G使得FG=AF,连接BG、AB.
在△ADF和△GCF中,
$\left\{\begin{array}{l}{AF=FG}\\{∠DFA=∠CFG}\\{DF=FC}\end{array}\right.$,
∴△ADF≌△GCF,
∴AF=FG,AD=CG,
∵∠DAE=∠CBE,∠DEA=∠CEB=60°,
∴△ADE∽△BCE,
∴$\frac{EB}{AE}$=$\frac{BC}{AD}$=$\frac{BC}{CG}$,
∴$\frac{BC}{EB}$=$\frac{CG}{AE}$,
∴∠GAB=∠CEB=60°,∵FA=FB,
∴△FAB是等边三角形
∵∠GCB=∠GCF+∠DCE+∠ECB=∠FDA+∠DCE+30°=30°+∠EDC+∠DCE+30°=60°+∠EDC+∠DCE,
∠AEB=360°-∠DEA-∠CEB-∠DEC=360°-60°-60°-(180°-∠EDC-∠DCE)=60°+∠EDC+∠DCE
∴GCB=∠AEB,
∴△GCB∽△AEB,
∴∠GBC=∠ABE,$\frac{AB}{BG}$=$\frac{EB}{BC}$
∴∠ABG=∠EBC=90°,
∵AF=FG,
∴FB=AF=FG,
∵$\frac{AB}{GB}=\frac{EB}{BC}$,∠ABG=∠EBC,
∴△ABG∽△EBC,
∴∠GAB=∠CEB=60°,
∵FA=FB,
∴△FAB是等边三角形.
点评 本题考查全等三角形的判定和性质、相似三角形的判定和性质、等边三角形的性质等知识,解题的关键是添加辅助线构造全等三角形或相似三角形,第二个问题比较难,用了多次相似三角形的判定和性质,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 时间 | 第一个月 | 第二个月 | 清仓时 |
| 单价(元) | 80 | 80-x | 40 |
| 销售量 | 200 | 200+10x | 800-200-(200+10x) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
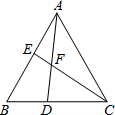 如图,在△ABC中,∠BAC=∠B=60°,AB=AC,点D、E分别是边BC、AB所在直线上的动点,且BD=AE,AD与BC交于点F.
如图,在△ABC中,∠BAC=∠B=60°,AB=AC,点D、E分别是边BC、AB所在直线上的动点,且BD=AE,AD与BC交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 作图并回答问题.
作图并回答问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com