��������1����֪�������ߵĶ��������Ϊ1����x=-
=1������֪��������������������У�������ʽ������������ߵĽ���ʽ��
��2������Ҫ������������ۣ���BOD�ס�BAC���BDO�ס�BAC������˼·����ͨ�����������εó��Ĺ���BD��BC��BO��BA�ı�����ϵʽ���BD�ij���Ȼ����ݡ�OBC=45�������������BD�ij����D������꣮
��3���������Ĺؼ����ҳ���������λ�ã�
�����ڡ�PCO����ǣ����Ҫ���ҳ���PCO��ֱ��ʱ��ֵ���Դ���ȷ��P�Ĵ���ȡֵ��Χ��ȥC���������߶Գ���ĶԳƵ�C�䣨2��3������ô��P��C���غ�ʱ����PCO=90�㣬��ˡ�PCO��Ϊ��ǣ���P��ĺ�����ش���2��
�ڵ���PCO=��ACOʱ������A�������������߶Գ���Ľ���ʽ��֪����ACO=��ECO�����ֱ��CE�������ߵĽ��㣨��C�⣩���Ǵ�ʱP���λ�ã��ݴ˿������ʱP��ĺ����꣮
��������������������ж����ɣ�
���
�⣺��1���߶��κ���ͼ��ĺ�����Ϊ1���ҹ��㣨2��3���ͣ�-3��-12����
����
���
��
��˶��κ����ı���ʽΪy=-x
2+2x+3��
��2���������ֱ��l��y=kx��k��0�����߶�BC���ڵ�D�������B��C�غϣ���ʹ����B��O��DΪ��������������BAC���ƣ�
��y=-x
2+2x+3����y=0������-x
2+2x+3=0��
���x
1=-1��x
2=3��
��A��-1��0����B��3��0����
��x=0����y=3��
��C��0��3����
�����O��ֱ��l��BC�ڵ�D������D��DE��x���ڵ�E��
�ߵ�B������Ϊ��3��0������C������Ϊ��0��3������A������Ϊ��-1��0����
��|AB|=4��|OB|=|OC|=3����OBC=45�㣮
��|BC|=
=3
��
Ҫʹ��BOD�ס�BAC���BDO�ס�BAC��
���С�B=��B����ֻ��
=���ٻ�
=�ڳ�����
���Ǣ٣�����|BD|=
=
=
��
����OBC=45�㣬
��|BE|=|DE|��
����Rt��BDE�У��ɹ��ɶ�����
��|BE|
2+|DE|
2=2|BE|
2=|BD|
2=��
��
2��
���|BE|=|DE|=
����ֵ��ȥ����
��|OE|=|OB|-|BE|=3-
=
��
���D��������
��
����
����D���������y=kx��k��0�������k=3��
������������ֱ��l�ĺ�������ʽΪy=3x��
�����ֱ��AC�ĺ�������ʽΪy=3x+3������ֱ��ACƽ�е�ֱ��l�ĺ�������ʽΪy=3x��
��ʱ��֪��BOD�ס�BAC�������ֱ��BC�ĺ�������ʽΪy=-x+3������y=3x��y=-x+3��õ�D������Ϊ��
��
����
���Ǣڣ�����|BD|=
=
=2
��
����OBC=45�㣬
��|BE|=|DE|��
����Rt��BDE�У��ɹ��ɶ�����
��|BE|
2+|DE|
2=2|BE|
2=|BD|
2=��2
��
2��
���|BE|=|DE|=2����ֵ��ȥ����
��|OE|=|OB|-|BE|=3-2=1��
���D��������1��2����
����D���������y=kx��k��0�������k=2��
������������ֱ��l�ĺ�������ʽΪy=2x��
�����ֱ��l��y=3x��y=2x���߶�BC���ڵ�D�������B��C�غϣ���
ʹ����B��O��DΪ��������������BAC���ƣ��ҵ�D������ֱ�Ϊ��
��
����1��2����
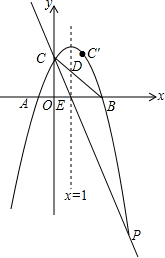
��3�������C��0��3����E��1��0����ֱ��y=kx+3��k��0����ö��κ�����ͼ���ڵ�P��
����E��1��0�����������y=kx+3��
���k=-3��
���ֱ�ߵĺ�������ʽΪy=-3x+3��
���P��������x��-3x+3����
������y=-x
2+2x+3����x
2-5x=0��
���x
1=5��x
2=0���������⣬��ȥ����
��x=5��y=-12��
���P��������5��-12����
��ʱ����ǡ�PCO=��ACO��
�֡߶��κ����ĶԳ���Ϊx=1��
���C���ڶԳ���ԳƵĵ�C'������Ϊ��2��3����
�൱x
p��5ʱ����ǡ�PCO����ACO��
��x
p=5ʱ����ǡ�PCO=��ACO��
��2��x
p��5ʱ����ǡ�PCO����ACO��

 ��ǡ�PCO���ACO�Ĵ�С������֤��������д����ʱ��P�ĺ�����xp��ȡֵ��Χ��
��ǡ�PCO���ACO�Ĵ�С������֤��������д����ʱ��P�ĺ�����xp��ȡֵ��Χ��  �⣺��1���߶��κ���ͼ��ĺ�����Ϊ1���ҹ��㣨2��3���ͣ�-3��-12����
�⣺��1���߶��κ���ͼ��ĺ�����Ϊ1���ҹ��㣨2��3���ͣ�-3��-12����


 ��ͼ����ƽ��ֱ������ϵxOy�У���ABC��A��B����������x���ϣ�����C��y��ĸ������ϣ���֪|OA|��|OB|=1��5��|OB|=|OC|����ABC�����S��ABC=15��������y=ax2+bx+c��a��0������A��B��C���㣮
��ͼ����ƽ��ֱ������ϵxOy�У���ABC��A��B����������x���ϣ�����C��y��ĸ������ϣ���֪|OA|��|OB|=1��5��|OB|=|OC|����ABC�����S��ABC=15��������y=ax2+bx+c��a��0������A��B��C���㣮 ��ͼ����ƽ��ֱ������ϵxOy�У�A��2��1����B��4��1����C��1��3�������ABC���ABDȫ�ȣ����D����Ϊ
��ͼ����ƽ��ֱ������ϵxOy�У�A��2��1����B��4��1����C��1��3�������ABC���ABDȫ�ȣ����D����Ϊ